cho A=x3-x2+2 . Tìm giá trị nguyên x để A là số nguyên dương.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 5 2018
Đáp án A
Ghi nhớ: Nếu hàm số 
liên tục trên đoạn 
và 
thì phương trình 
có ít nhất một nghiệm nằm trong khoảng 
.
PT
1
CM
16 tháng 8 2018
Hướng dẫn giải:
Điều kiện xác định của phân thức: x ≠ 1
Ta có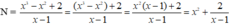 
Để N nguyên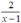 
nguyên ⇒ x - 1 là ước của 2
Ư ( 2 ) = 1 ; - 1 ; 2 ; - 2
x – 1 = 1 ⇒ x =2 (thỏa mãn điều kiện xác định);
x - 1 = -1 ⇒ x = 0 (thỏa mãn điều kiện xác định);
x - 1 = 2 ⇒ x = 3 (thỏa mãn điều kiện xác định);
x - 1 = -2 ⇒ x = -1 (thỏa mãn điều kiện xác định);
Vậy với x ∈ { -1;0;2;3 } thì phân thức N nhận giá trị nguyên
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
\(x^4-x^3+6x^2-x+a=x^2\left(x^2-x+5\right)+x^2-x+a\)
Do \(x^2\left(x^2-x+5\right)\) chia hết \(x^2-x+5\)
\(\Rightarrow x^2-x+a\) chia hết \(x^2-x+5\)
\(\Rightarrow a=5\)
PT
1
NT
0
NT
0
17 tháng 12 2023
a: \(A=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)
\(=\left(2x\right)^3-1^3-7x^3-7\)
\(=8x^3-1-7x^3-7=x^3-8\)
b: Thay x=-1/2 vào A, ta được:
\(A=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)
18 tháng 12 2023
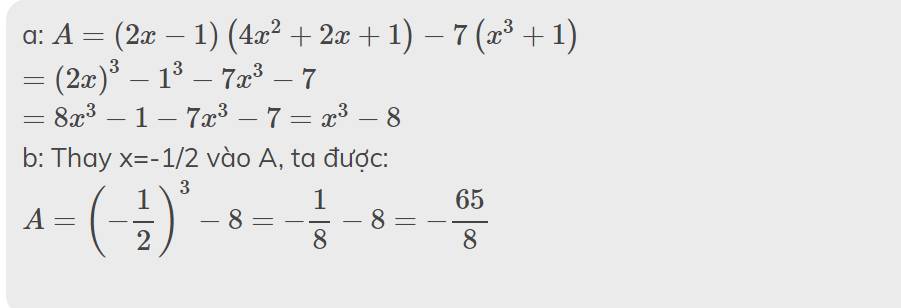
c: \(A=x^3-8=\left(x-2\right)\left(x^2+2x+4\right)\)
Để A là số nguyên tố thì x-2=1
=>x=3
26 tháng 12 2021
b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)
Có: \(A=x^3-x^2+2\)
\(=x^3+1-x^2+1\)
\(=\left(x+1\right)\left(x^2-x+1\right)-\left(x+1\right)\left(x-1\right)\)
\(=\left(x+1\right)\left(x^2-2x+2\right)\)
A là số dương
<=> \(\left(x+1\right)\left(x^2-2x+2\right)>0\)
Vì \(x^2-2x+2=\left(x-1\right)^2+1>0\)
=> \(\left(x+1\right)>0\)
<=> x > - 1
A là số nguyên => x nguyên
Vậy để A là số nguyên dương thì x là số nguyên và x > -1.