cho tam giác ABC cân tại A gọi M và N lần lượt là trung điểm của BC và AC.biết AB=20cm. a)tính MN b)gọi D là điểm đối xứng của A qua M.cm ABDC là hình thoi C)lấy E đối xứng với M qua N.Gọi I là trung điểm của MC.cm I,E,D thẳng hàng D)kẻ EH vuông góc với AC tại H,trên tia dối của EH lấy F sao cho EF=AC.chứng minh góc AMF =45 độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


hình mình vẽ tượng trưng thôi nha
đề của bạn 1 số chỗ hơi nhầm đó nha.
a)
dựa theo công thức tính diện tích tam giác, ta có:
S\(\Delta\)ABC = \(\dfrac{1}{2}.12.16=96\left(cm^2\right)\)
ta có:
AN = NC ; AM = MB
=> MN là đường trung bình của tam giác ABC
do đó MN//= \(\dfrac{1}{2}\)BC
=> MN = 6 cm
b) ta có:
AM = MB ; HM = ME
=> AHBE là hình bình hành
Mà ta lại thấy góc AHB vuông
=> AHBE là hình chữ nhật
c) ta có:
AH= HF ; CH = HB
=> ABFC là hình bình hành
Mà ta thấy AF \(\perp\) CB
suy ra ABFC là hình thoi.
d) mk k hỉu cái đề cho lắm nên thôi nha.![]()
chúc bạn học tốt

a: \(S_{ABC}=\dfrac{AH\cdot BC}{2}=12\cdot8=96\left(cm^2\right)\)
Xét ΔBAC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN=BC/2=6(cm)
b: Xét tứ giác AHBE có
M là trung điểm của AB
M là trung điểm của HE
Do đó:AHBE là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBE là hình chữ nhật
c: Xét tứ giác ABFC có
H là trung điểm của AF
H là trung điểm của BC
Do đó: ABFC là hình bình hành
mà AB=AC
nên ABFC là hình thoi

câu b
b) => EB = FC = EA = AF
nối ME
nối MF
vì tam giác BMA vuông tại M vs ME cắt tai trung điểm AB
=> ME = EA
tương tự vs tam giác AMC vuông tại M
=> AE = EM = MF = AF
=> AEMF là hình thoi
bài này quá dễ
a) vì D là điểm đối xứng vs A qua BC
=> AD vuông góc vs BC
AM = MD
tam giác BAM = CDM
=> AB = DC
tam giác AMC = DMB
=> AC = BD
mà AC = AB
=> AB = AC = BD = DC
=> ABDC là hình thoi

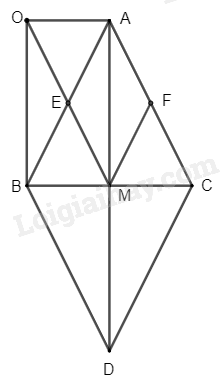
a) Xét tứ giác \(ABDC\) có:
\(M\) là trung điểm của \(BC\) (gt)
\(M\) là trung điểm của \(AD\) (do \(D\) đối xứng với \(A\) qua \(BC\))
Suy ra \(ABDC\) là hình bình hành
b) Do \(\Delta ABC\) cân tại \(A\), có \(AM\) là trung tuyến (gt)
Suy ra \(AM\) là đường cao, trung trực, phân giác
Suy ra \(AM\) vuông góc \(BM\) và \(CM\)
Xét tứ giác \(OAMB\) ta có:
\(E\) là trung điểm của \(OM\) và \(AB\) (gt)
Suy ra \(OAMB\) là hình bình hành
Suy ra \(OB\) // \(AM\); \(OA\) // \(MB\); \(OA = BM\); \(OB = AM\)
Mà \(AM \bot BM\) (cmt)
Suy ra: \(AM \bot OA\); \(OB \bot MB\)
Mà \(AM\) // \(OB\) (cmt)
Suy ra \(OB \bot OA\)
Xét \(\Delta AOB\) và \(\Delta MBO\) (các tam giác vuông) ta có:
\(\widehat {{\rm{AOB}}} = \widehat {{\rm{OBM}}} = 90^\circ \)
\(AO = MB\) (cmt)
\(OB = AM\) (cmt)
Suy ra \(\Delta AOB = \Delta MBO\) (c-g-c)
Suy ra \(OM = AB\)
c) \(OM = AB\) (cmt)
Mà \(EM = EO = \frac{1}{2}OM\); \(EA = EB = \frac{1}{2}AB\)
Suy ra \(EO = EA = EM = EB\) (1)
Xét \(\Delta ABC\) cân ta có: \(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) và \(AB = AC\)
Mà \(EA = EB = \frac{1}{2}AB\); \(FA = FC = \frac{1}{2}AC\) (gt)
Suy ra \(AE = EB = FA = FM\) (2)
Xét \(\Delta BEM\) và \(\Delta CMF\) ta có:
\(BE = CF\) (cmt)
\(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) (cmt)
\(BM = CM\) (gt)
Suy ra \(\Delta BEM = \Delta CFM\) (c-g-c)
Suy ra \(EM = FM\) (3)
Từ (1), (2), (3) suy ra \(AE = AF = FM = ME\)
Suy ra \(AEMF\) là hình thoi