gấp gấp nói hộ e abc thôi ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2,\\ a,=2x^2+4x-3x-6-2x^2-4x-2=-3x-8\\ b,=\left[x-2+2\left(x+1\right)\right]^2=\left(x-2+2x+2\right)^2=9x^2\)



Xét tứ giác GHKI có
GH//KI
GH=KI
Do đó: GHKI là hình bình hành
Suy ra: GI=HK

\(\dfrac{5}{8}+\dfrac{3}{8}x=1\dfrac{1}{8}\)
\(\Rightarrow\dfrac{5}{8}+\dfrac{3}{8}x=\dfrac{9}{8}\)
\(\Rightarrow\dfrac{3}{8}x=\dfrac{9}{8}-\dfrac{5}{8}\)
\(\Rightarrow\dfrac{3}{8}x=\dfrac{4}{8}\)
\(\Rightarrow x=\dfrac{4}{8}:\dfrac{3}{8}\)
\(\Rightarrow x=\dfrac{4}{8}\cdot\dfrac{8}{3}=\dfrac{4}{3}\)
\(---\)
\(\dfrac{1}{2}-\left(\dfrac{1}{3}x-2\right)=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{1}{3}x-2=\dfrac{1}{2}-\dfrac{2}{3}\)
\(\Rightarrow\dfrac{1}{3}x-2=-\dfrac{1}{6}\)
\(\Rightarrow\dfrac{1}{3}x=-\dfrac{1}{6}+2\)
\(\Rightarrow\dfrac{1}{3}x=\dfrac{11}{6}\)
\(\Rightarrow x=\dfrac{11}{6}:\dfrac{1}{3}\)
\(\Rightarrow x=\dfrac{11}{6}\cdot3=\dfrac{11}{2}\)
\(---\)
\(\left(3x+4\right)\left(2x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3x+4=0\\2x-3=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}3x=-4\\2x=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{4}{3}\\x=\dfrac{3}{2}\end{matrix}\right.\)
\(--\)
\(-4+4x=9x-14\)
\(\Rightarrow4x-9x=-14+4\)
\(\Rightarrow-5x=-10\)
\(\Rightarrow x=\left(-10\right):\left(-5\right)=2\)
\(---\)
\(\left\{\left[\left(\dfrac{1}{25}-0,6\right)^2:\dfrac{49}{125}\right]\cdot\dfrac{5}{6}\right\}-\left[\left(\dfrac{-1}{3}\right)+\dfrac{1}{2}\right]\)
\(=\left[\left(-\dfrac{14}{25}\right)^2\cdot\dfrac{125}{49}\right]\cdot\dfrac{5}{6}-\dfrac{1}{6}\)
\(=\left(\dfrac{196}{625}\cdot\dfrac{125}{49}\right)\cdot\dfrac{5}{6}-\dfrac{1}{6}\)
\(=\dfrac{4}{5}\cdot\dfrac{5}{6}-\dfrac{1}{6}\)
\(=\dfrac{4}{6}-\dfrac{1}{6}\)
\(=\dfrac{3}{6}\)
\(=\dfrac{1}{2}\)
\(Toru\)

2.1
ĐKXĐ: \(x\ge-\dfrac{1}{16}\)
\(x^2-x-20-2\left(\sqrt{16x+1}-9\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4\right)-\dfrac{32\left(x-5\right)}{\sqrt{16x+1}+9}=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4-\dfrac{32}{\sqrt{16x+1}+9}\right)=0\) (1)
Do \(x\ge-\dfrac{1}{16}\Rightarrow\left\{{}\begin{matrix}\dfrac{32}{\sqrt{16x+1}+9}< \dfrac{32}{9}\\x+4\ge-\dfrac{1}{16}+4=\dfrac{63}{16}>\dfrac{32}{9}\end{matrix}\right.\)
\(\Rightarrow x+4-\dfrac{32}{\sqrt{16x+1}+9}>0\)
Nên (1) tương đương:
\(x-5=0\)
\(\Leftrightarrow x=5\)
Câu 2.2, 2.3 đề lỗi không dịch được

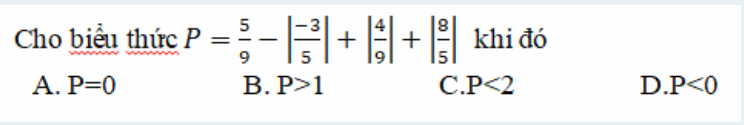

 Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!
Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!

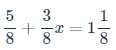
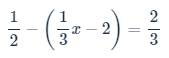
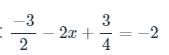
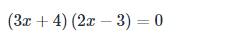
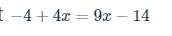
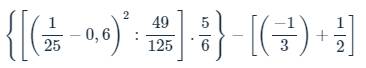 ghi kết quả thôi ạ , k phải trình bày ạ , e cần gấp ạ !!!!!
ghi kết quả thôi ạ , k phải trình bày ạ , e cần gấp ạ !!!!!


D
câu d á