Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có abc = 3. (a+b+c)
⇒
⇒abc chia hết cho 3
Giả sử a chia hết cho 3. Do a là số nguyên tố
⇒
⇒ a=3
3bc=3(3+b+c)
⇒
⇒ bc=3+b+c
bc-b = 3+c
⇒
⇒ b(c-1) = 4+(c-1)
⇒
⇒ (b-1)(c-1) = 4
⇒
⇒ (b,c)
∈
∈ {(3,3);(2,5)}
Vậy (a,b,c
∈
∈ {(3,3,3) ; (2,3,5)}

Ta có abc = 3. (a+b+c) \(\Rightarrow\)abc chia hết cho 3
Giả sử a chia hết cho 3. Do a là số nguyên tố \(\Rightarrow\) a=3
3bc=3(3+b+c) \(\Rightarrow\) bc=3+b+c
bc-b = 3+c \(\Rightarrow\) b(c-1) = 4+(c-1) \(\Rightarrow\) (b-1)(c-1) = 4
\(\Rightarrow\) (b,c) \(\in\) {(3,3);(2,5)}
Vậy (a,b,c) \(\in\) {(3,3,3) ; (2,3,5)}


Bạn clink chuột vào đây có bài này tớ làm rồi Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath

Giả sử tồn tại các số nguyên a; b; c thỏa mãn:
a.b.c + a = -625 ; a.b.c + b = -633 và a.b.c + c = -597
Xét từng điều kiện ta có:
a.b.c + a = a.(b.c + 1) = -625
a.b.c + b = b.(a.c + 1) = -633
a.b.c + c = c.(a.b + 1) = -597
Chỉ có hai số lẻ mới có tích là một số lẻ \(\Rightarrow\) a; b; c đều là số lẻ \(\Rightarrow\) a.b.c cũng là số lẻ.
Khi đó a.b.c + a là số chẵn, không thể bằng -625 (số lẻ)
Vậy không tồn tại các số nguyên a; b; c thỏa mãn điều kiện đề bài.

Từ abc = 3(a + b + c) suy ra a chia hết cho 3 hoạc b chia hết cho 3 hoặc c chia hết cho 3. Vậy
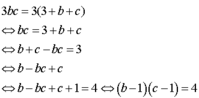
Do b và c là các sốnguyên tố b - 1 ≥ 1 ; c - 1 ≥ 1 và b – 1 , c – 1 là ước của 4 vậy chúng nhận 1 trông các giá trị là 1, 2, 4. Vậy ta có các trường hợp sau:
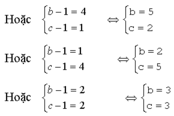
Các cặp số (a, b, c) phải Tìm là : (3, 3, 3) ; (3, 2, 5) ; (3, 5, 2) ; (5, 3, 2 ) ; (5, 2, 3) ; (2, 3, 5) ; (2, 5, 3)