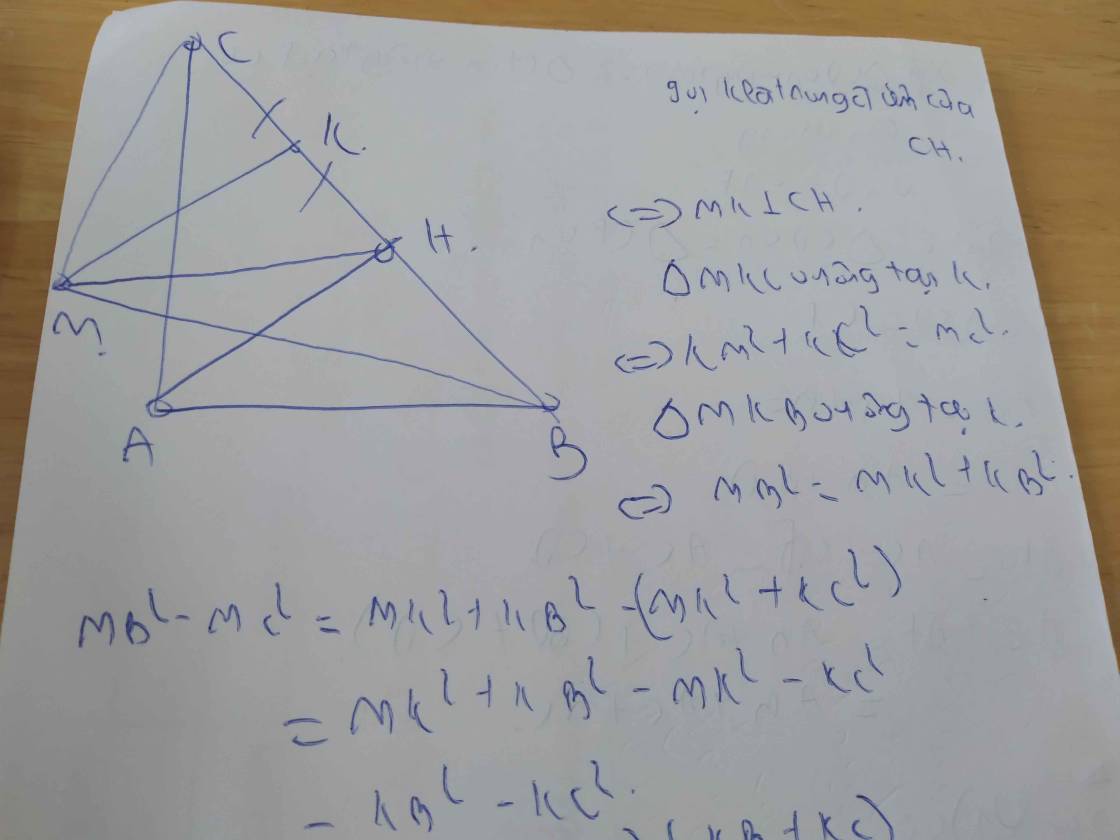
Cho tam giác ABC có BC=a Tìm M sao cho vecto MA.MB-MA.MB=-a2 - MB2 + MC2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 1 2021
tham khảo
https://cungthi.online/cau-hoi/cho-tam-giac-abc-tap-hop-nhung-diem-m-thoaman-4mambmc-30238-1652.html
7 tháng 3 2021
Gọi G là trọng tâm của ΔABC
⇒ \(3\overrightarrow{MG}=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\)
⇒ \(MA^2+MB^2+MC^{2^{ }}+2VT=9MG^2\)
⇒ VT = 9MG2 - MA2 + MB2 + MC2
⇒ \(\dfrac{a^2}{6}\) = 9MG2 - MA2 + MB2 + MC2
MA2 + MB2 + MC2
\(=\left(\overrightarrow{MG}+\overrightarrow{GA}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GB}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GC}\right)^2\)
= 3MG2 + 2\(\overrightarrow{MG}\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)+ GA2 + GB2 + GC2
= 3MG2 + \(GA^2+GB^{2^{ }}+GC^2\)
do \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
Vậy ta có
\(\dfrac{a^2}{6}=6MG^2-GA^2-GB^2-GC^2\)
⇔ \(\dfrac{a^2}{6}+\left(GA^2+GB^2+GC^2\right)=6MG^2\)(1)
Lưu ý, GA,GB,GC lần lượt bằng \(\dfrac{2}{3}\) độ dài các đường trung tuyến kẻ từ A,B,C. Nhưng do ΔABC đều nên chúng sẽ lần lượt bằng \(\dfrac{2}{3}\) đường cao kẻ từ A,B,C (đặt là ha ; hb; hc)
Dễ dàng tìm được ha = hb = hc = \(\dfrac{a\sqrt{3}}{2}\)
⇒ GA = GB = GC = \(\dfrac{a\sqrt{3}}{3}\)
⇒ GA2 = GB2 = GC2 = \(\dfrac{a^2}{3}\)
⇒ GA2 + GB2 + GC2 = a2
Thay vào (1)
\(\dfrac{a^2}{6}+a^2=3MG^2\) ⇔ MG2 = \(\dfrac{7a^2}{18}\)
⇔ MG = \(\dfrac{a\sqrt{14}}{6}\)
Vậy R = \(\dfrac{a\sqrt{14}}{6}\)
Ai xem hộ sai chỗ nào vs
2 tháng 3 2021
a, Gọi I là trọng tâm của ΔABC
⇒ \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\)
MA2 + MB2 + MC2 = k2
⇔ 3MI2 + 2\(\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}\right)+AB^2+AC^2+BC^2\) = k2
⇔ 3MI2 = k2 - 1014
⇔ MI = \(\sqrt{\dfrac{k-1014}{3}}\) = const
Vậy M thuộc \(\left(I;\sqrt{\dfrac{k-1014}{3}}\right)\)
CM
27 tháng 6 2017
a) Gọi O là tâm đường tròn ngoại tiếp. Do tam giác ABC là tam giác đều nên O đồng thời là trọng tâm tam giác đều ABC.
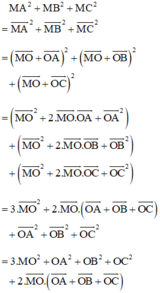
Lại có:
+ O là trọng tâm tam giác nên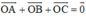 
+ Bán kính đường tròn ngoại tiếp tam giác:
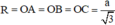
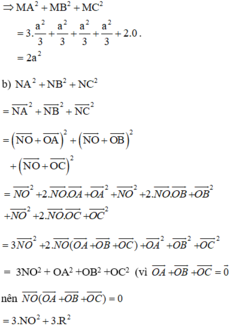
Ta có: NA2 + NB2 + NC2 ngắn nhất
⇔ NO2 ngắn nhất vì R không đổi
⇔ NO ngắn nhất
⇔ N là hình chiếu của O trên d.
CM
10 tháng 1 2019
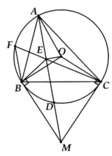
a, O B M ^ = O E M ^ = 90 0
=> Tứ giác OEBM nội tiếp
b, Chứng minh được: ∆ABM:∆BDM (g.g) => M B 2 = M A . M B
c, DOBC cân tại O có OM vừa là trung trực vừa là phân giác
=> M O C ^ = 1 2 B O C ^ = 1 2 s đ B C ⏜
Mà B F C ^ = 1 2 B C ⏜ => M O C ^ = B F C ^
d, O E M ^ = O C M ^ = 90 0 => Tứ giác EOCM nội tiếp
=> M E C ^ = M O C ^ = B F C ^ mà 2 góc ở vị trí đồng vị => FB//AM
