Cho tam giác ABC vuông tại A AB = 6 AC = 8 phép vị tự tâm A tỷ số 3/2 đến B thành B'; biến C thành C' tính bán kính R của đường tròn ngoại tiếp tam giám AB'C'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
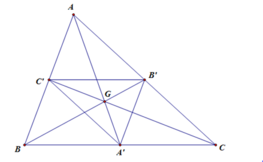
G A → = − 2 G A ' → ⇒ V G , − 2 A ' = A G B → = − 2 G B ' → ⇒ V G , − 2 B ' = B G C → = − 2 G C ' → ⇒ V G , − 2 C ' = C ⇒ V G , − 2 Δ A ' B ' C ' = Δ A B C

Đáp án B
A’ = V G ; k ( A ) => − 2 G A ' → = G A → =>Tỉ số vị tự k = – 2

Đáp án A
B = V A ; k ( M ) và 2 M A → = A B →
C = V A ; k ( N ) và 2 N A → = A C →
=>k = 2

2: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
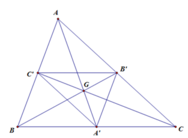
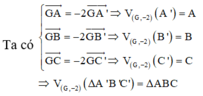
Tính được BC=10
O là trung điểm BC suy ra AO=5
\(V_{\left(A;\frac{3}{2}\right)}:B\rightarrow B',C\rightarrow C',O\rightarrow O'\)
(O' là tâm đường tròn ngoại tiếp tam giác AB'C')
\(\Rightarrow\overrightarrow{AO'}=\frac{3}{2}\overrightarrow{AO}\Rightarrow\left|\overrightarrow{AO'}\right|=\left|\frac{3}{2}\right|\left|\overrightarrow{AO}\right|\Rightarrow AO'=\frac{3}{2}AO=7,5\)
=>R=7,5