cho 2 số thực dương x,y thỏa mãn: x+3y\(\ge\) 6. tìm giá trị nhỏ nhất của biểu thức P= x+y+\(\frac{6}{x}\)+2011
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
2 tháng 1 2021
Mình nghĩ phần phân thức là $3x+3y+2z$ thay vì $3x+3y+3z$. Nếu là vậy thì bạn tham khảo lời giải tại link sau:
Cho x, y, z là các số thực dương thỏa mãn đẳng thức xy yz zx=5. Tìm GTNN của biểu thức \(P=\frac{3x 3y 2z}{\sqrt{6\left(... - Hoc24
MT
2 tháng 1 2021
mình cảm ơn bạn nhiều ạ <3 bạn có thể giúp mình mấy câu mình vừa đăng không
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
\(P=\dfrac{x^2+y^2+6}{x+y}=\dfrac{x^2+y^2+2xy+4}{x+y}=\dfrac{\left(x+y\right)^2+4}{x+y}=x+y+\dfrac{4}{x+y}\)
\(P\ge2\sqrt{\left(x+y\right).\dfrac{4}{x+y}}=4\)
\(P_{min}=4\) khi \(x=y=1\)
6 tháng 4 2017
\(Q=2x^2+\frac{6}{x^2}+3y^2+\frac{8}{y^2}\)
\(=\left(2x^2+\frac{2}{x^2}\right)+\left(3y^2+\frac{3}{y^2}\right)+\left(\frac{4}{x^2}+\frac{5}{y^2}\right)\)
Ta có :
\(2x^2+\frac{2}{x^2}\ge2\sqrt{2x^2.\frac{2}{x^2}}=2\sqrt{2.2}=4\) (BĐT AM - GM)
Dấu "=" xảy ra <=> \(2x^2=\frac{2}{x^2}\Rightarrow x=1\)
\(3y^2+\frac{3}{y^2}\ge2\sqrt{3y^2.\frac{3}{y^2}}=2\sqrt{3.3}=6\) (BĐT AM - GM)
Dấu "=" xảy ra <=> \(3y^2=\frac{3}{y^2}\Rightarrow y=1\)
\(\Rightarrow Q=\left(2x^2+\frac{2}{x^2}\right)+\left(3y^2+\frac{3}{y^2}\right)+\left(\frac{4}{x^2}+\frac{5}{y^2}\right)\ge4+6+9=19\)
Dấu "=" xảy ra <=> x = y = 1
Vậỵ GTNN của Q là 19 tại x = y = 1
BN
0
CM
29 tháng 3 2018
ĐK:
Ta có
log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4
Xét hàm số f ( x ) = log 3 t + 3 t t > 0
có f ' ( t ) = 1 t ln 3 + 3 > 0 ; ∀ t > 0 nên hàm số đồng biến trên 0 ; + ∞
Kết hợp (*) suy ra
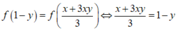
Xét P = x + y ⇒ x = P - y thay vào (**) ta được
Ta tìm giá trị nhỏ nhất của g ( y ) = 3 y 2 - 2 y + 3 3 y + 1 trên (0;1)
Ta có
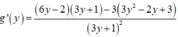
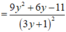
Giải phương trình
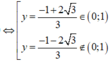
Lại có g ' ( y ) < 0 ∀ y ∈ 0 ; - 1 + 2 3 3
và g ' ( y ) > 0 ∀ y ∈ - 1 + 2 3 3 ; 1
Hay g'(y) đổi dấu từ âm sang dương tại y = - 1 + 2 3 3 nên
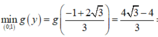
⇒ P m i n = 4 3 - 4 3
Chọn đáp án A.