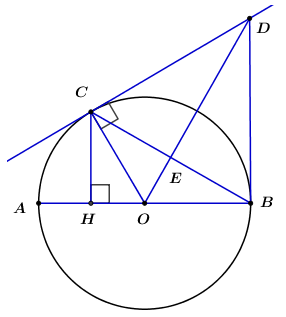
Cho (O) đường kính AB lấy điểm C thuộc đường tròn sao cho AC = AO kẻ CH thuộc AB O thuộc BC tiếp tuyến tại C cắt OD ở E
a) Chứng minh 4 điểm C,H,O,D cùng thuộc một đường tròn
b) chứng minh OD ,OE=AH ,AB
c) Chứng minh AB là tiếp tuyến của đường tròn (O)