Giải phương trình bằng phương pháp đặt ẩn phụ
\(x^2+5x+7=6\sqrt{x^3+7x}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NQ
0
PT
1
CM
2 tháng 11 2018
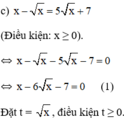
Khi đó (1) trở thành: t2 – 6t – 7 = 0 (2)
Giải (2): Có a = 1; b = -6; c = -7
⇒ a – b + c = 0
⇒ (2) có nghiệm t1 = -1; t2 = -c/a = 7.
Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.
+ Với t = 7 ⇒ √x = 7 ⇔ x = 49 (thỏa mãn).
Vậy phương trình đã cho có nghiệm x = 49.
BL
2
T
3 tháng 12 2019
ĐK: \(x\ge-1\)
PT \(\Leftrightarrow x^2+5x+7=7\sqrt{\left(x+1\right)\left(x^2-x+1\right)}\)
Đặt \(\sqrt{x+1}=a;\sqrt{x^2-x+1}=b\Rightarrow6a^2+b^2=x^2+5x+7\)
PT \(\Leftrightarrow6a^2+b^2=7ab\Leftrightarrow\left(a-b\right)\left(6a-b\right)=0\)
*Với a = b \(\Leftrightarrow\sqrt{x^2-x+1}=\sqrt{x+1}\Leftrightarrow x^2-x+1=x+1\)
\(\Leftrightarrow x\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\left(TM\right)\\x=2\left(TM\right)\end{matrix}\right.\)
*Với \(6a=b\Leftrightarrow\sqrt{x^2-x+1}=6\sqrt{x+1}\)
\(\Leftrightarrow x^2-x+1=36x+36\)
\(\Leftrightarrow x^2-37x-35=0\) .Dùng delta tính nốt:v
Vậy..... (có 4 nghiệm thỏa mãn)...
BL
0
LY
1
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
ĐKXĐ: \(x\ge1\)
Do \(\sqrt{x-\sqrt{x^2-1}}.\sqrt{x+\sqrt{x^2-1}}=\sqrt{x^2-x^2+1}=1\)
Đặt \(\sqrt{x-\sqrt{x^2-1}}=t\Rightarrow\sqrt{x+\sqrt{x^2-1}}=\dfrac{1}{t}\)
Phương trình trở thành:
\(t+\dfrac{1}{t}=2\Rightarrow t^2-2t+1=0\Rightarrow t=1\)
\(\Rightarrow\sqrt{x-\sqrt{x^2-1}}=1\Leftrightarrow x-\sqrt{x^2-1}=1\)
\(\Leftrightarrow x-1=\sqrt{x^2-1}\)
\(\Rightarrow x^2-2x+1=x^2-1\)
\(\Rightarrow x=1\) (thỏa mãn)
LY
1
30 tháng 1
\(\sqrt{x^2-x+1}+\sqrt{x^2-9x+9}=2x\)
=>\(\sqrt{x^2-x+1}-x+\sqrt{x^2-9x+9}-x=0\)
=>\(\dfrac{x^2-x+1-x^2}{\sqrt{x^2-x+1}+x}+\dfrac{x^2-9x+9-x^2}{\sqrt{x^2-9x+9}+x}=0\)
=>\(\left(-x+1\right)\left(\dfrac{1}{\sqrt{x^2-x+1}+x}+\dfrac{9}{\sqrt{x^2-9x+9}+x}\right)=0\)
=>-x+1=0
=>x=1
PT
1
