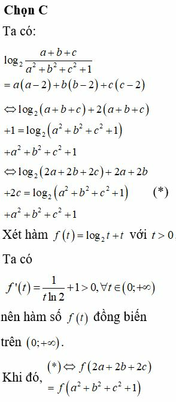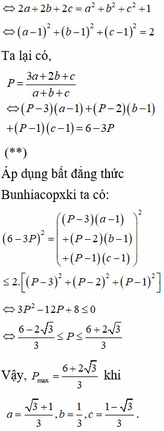tìm giá trị thích hợp của a,b : aa,bxa,b =aa,bb
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


abx99=aabb=11xa0b =>abx9=a0b =>90a+9b=100a+b =>10a=8b =>5a=4b => a=4 va b=5.

abx99=aabb=11xa0b
=>abx9=a0b
=>90a+9b=100a+b
=>10a=8b
=>5a=4b
=> a=4 va b=5.

aa x bb = 3267
(10a+a) x (10b+b) = 3267
11a x 11b = 3267
a x b = 3267 : 11 : 11 = 27
Có : 27 = 1 x 27 = 3 x 9
=> a=9;b=3 ( vì a,b là các chữ số và a > b > 1 )
Tk mk nha
\(\overline{aa}\times\overline{bb}=11a\times11b=121ab=3267\)
\(\Rightarrow ab=27=3.9=9.3\)
Vậy a=3,b=9 hoặc a=9,b=3

Lời giải:
\(\overline{aa}+\overline{bb}+\overline{cc}=\overline{bac}\)
\(11.a+11.b+11c=100b+10a+c\)
\(89b=a+10c=\overline{ca}\)
Vì $\overline{ca}$ là số có 2 chữ số nên $89b$ cũng chỉ có 2 chữ số. Nếu $b\geq 2$ thì $89b>100$ (vô lý) nên $b< 2$
Nếu $b=1$ thì $\overline{ca}=89\Rightarrow c=8; a=9$
Nếu $b=0$ thì $\overline{ca}=0\Rightarrow c=a=0$ (loại)
Vậy $a=9; b=1; c=8$

Ta biết tập nghiệm của phương trình ax + by = c được biểu diễn bằng đường thẳng ax + by = c và tập nghiệm của phương trình a'x + b'y = c' được biểu diễn bằng đường thẳng a'x + b'y = c'.