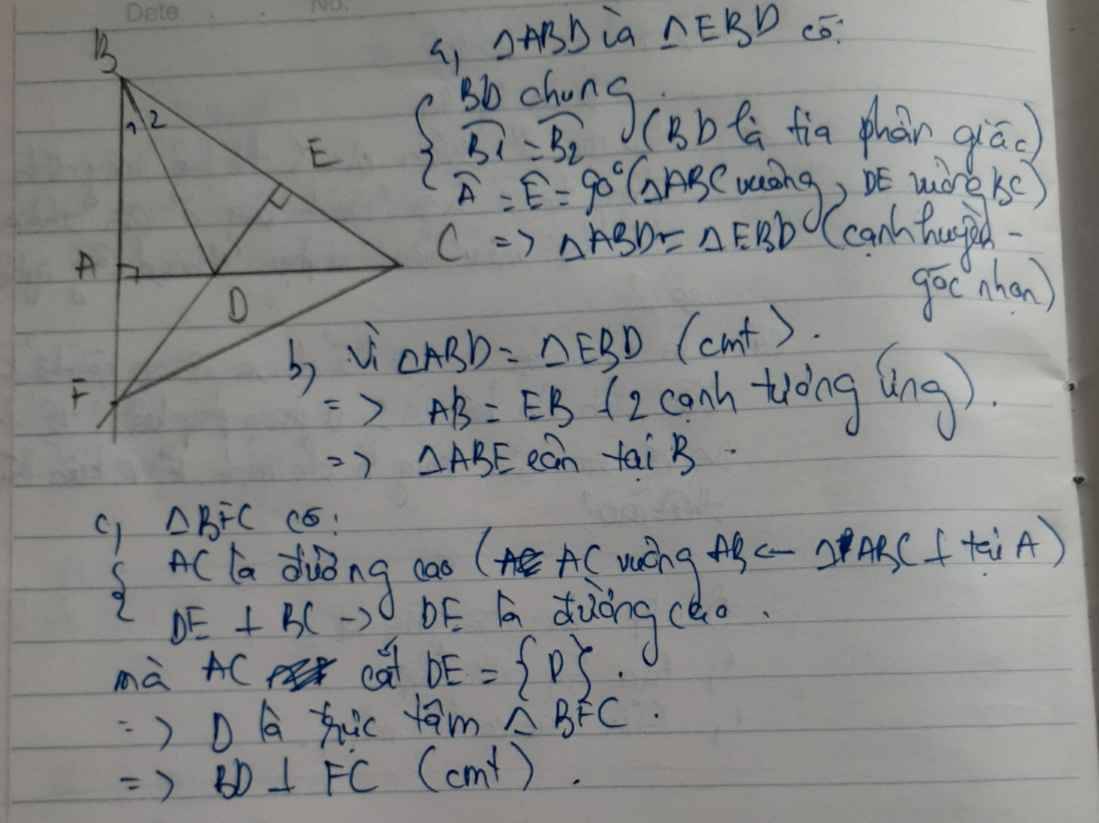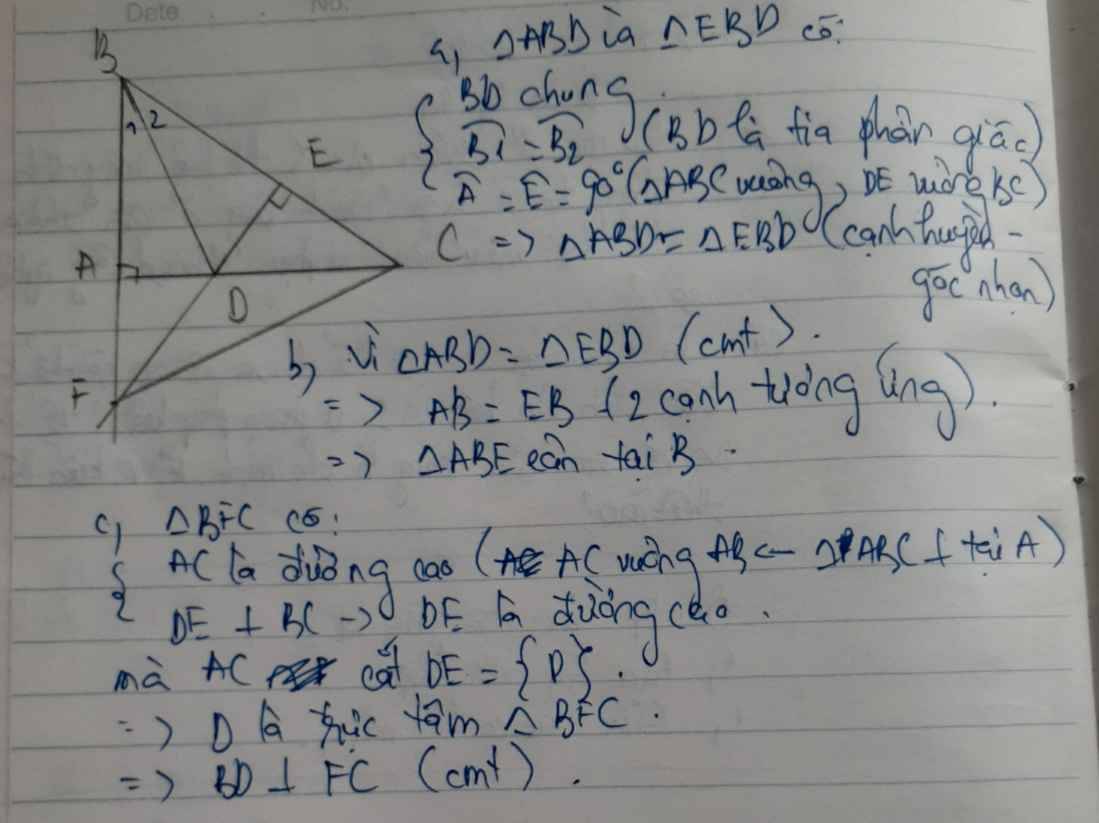Tam giác ABC vuông tại A (AB > AC) tia phân giác <ACB căt AB tại D. E thuôc BC, CE = CA
a) \(< ABC=48^0\). Tính <ABC
b) Chưng minh: DA = DE
c) CD vuông góc AE
d) Tư C vẽ đương thăng d vuông góc vơí AC tại C. Tư A vẽ đương thăng song song vơí CD căt d tại M. Chưng minh: AM = CD
* Lưu ý: Làm câu d) nhé....mâý câu khác mình biêt làm rôi....Help me...3 ticks