Cho BNN 2 chiều có hàm mật độ là:
f(x,y) = 0 nếu x^2+y^2>1
= 1/pi nếu x^2+y^2<=1
Tìm các hàm mật độ f(y/x) và g(x/y)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(F'_x=\frac{1}{\pi\left(1+x^2\right)}\left(\frac{1}{\pi}arctgy+\frac{1}{2}\right)\) \(\forall x,y\)
\(\Rightarrow F"_{xy}=\frac{1}{\pi\left(1+x^2\right)}.\frac{1}{\pi\left(1+y^2\right)}=\frac{1}{\pi^2\left(1+x^2+y^2+x^2y^2\right)}\)
\(\Rightarrow\)Hàm mật độ của BNN hai chiều (X, Y) là
\(f\left(x,y\right)=\frac{1}{\pi^2\left(1+x^2+y^2+x^2y^2\right)}\)

Vì mọi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x

a) Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \cot \left( { - x} \right) = - \cot x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \cot x\) là hàm số lẻ.
b)
\(x\) | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\frac{{3\pi }}{4}\) | \(\frac{{5\pi }}{6}\) |
\(\cot x\) | \(\sqrt 3 \) | \(1\) | \(\frac{{\sqrt 3 }}{3}\) | \(0\) | \( - \frac{{\sqrt 3 }}{3}\) | \( - 1\) | \( - \sqrt 3 \) |
c) Từ đồ thị trên, ta thấy hàm số \(y = \cot x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\), tập giá trị là \(\mathbb{R}\) và nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\).

Trong bảng ta thấy ứng với mỗi giá trị của x ta luôn xác định được chỉ một giá trị của y. Theo định nghĩa thì y là hàm số của đại lượng x. Ở đây giá trị của y không đổi nên hàm số là hàm hằng.

Cho hàm số y=f(x)y=f(x) có đạo hàm và liên tục trên [0;π2][0;π2]thoả mãn f(x)=f′(x)−2cosxf(x)=f′(x)−2cosx. Biết f(π2)=1f(π2)=1, tính giá trị f(π3)f(π3)
A. √3+1/2 B. √3−1/2 C. 1−√3/2 D. 0

a)
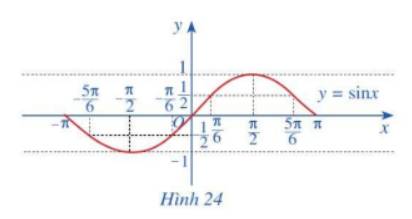
x | \( - \pi \) | \( - \frac{{5\pi }}{6}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{6}\) | 0 | \(\frac{\pi }{6}\) | \(\frac{\pi }{2}\) | \(\frac{{5\pi }}{6}\) | \(\pi \) |
\(y = \sin x\) | 0 | \( - \frac{1}{2}\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 |
b) Trong mặt phẳng Oxy, hãy biểu diễn các điểm \(\left( {x;y} \right)\) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\sin x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) với nối lại ta được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\)(Hình 24).
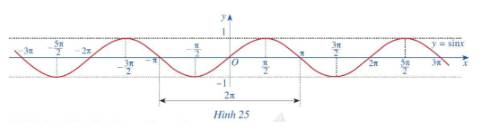
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \sin x\)trên R được biểu diễn ở Hình 25.