cho các số thực x,y,z khác 0 thỏa mãn 3x = 2y = 12-z.tính giá trị của biểu thức P= xy+yz+2zx
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 5 2019
Đáp án C
Từ 3 x = 4 x = 12 − x x = log 3 a y = log 4 a z = − log 12 a ⇒ P = log 3 a log 4 a − log 4 a log 12 a − log 12 a log 3 a
1
log
a
3
log
a
4
−
1
log
a
4
log
a
12
−
1
log
a
12
log
a
3
=
log
a
12
−
log
a
3
−
log
a
4
log
a
3
log
a
4
log
a
12
=
log
a
1
log
a
3
log
a
4
log
a
12
=
0
20 tháng 2 2022
\(\dfrac{x+y}{z}+\dfrac{y+z}{x}+\dfrac{x+z}{y}=\dfrac{x^2y+xy^2+y^2z+yz^2+x^2z+xz^2}{xyz}=\dfrac{-3xyz}{xyz}=-3\)
đề cho xy+yz+xz=0 nhân cả 2 vế với -z
=>-xyz-\(z^2\left(y+x\right)\)=0
=>-xyz=\(z^2x+z^2y\)
cmtt bạn nhân với -y và -z
=>-3xyz=\(x^2y+xy^2+y^2z+yz^2+x^2z+xz^2\)
VT
12 tháng 9 2017
ta có xy+yz+zx=0=> \(\frac{xy+yz+zx}{xyz}=0\)
\(\Rightarrow\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\)
đặt \(\frac{1}{x}=a,\frac{1}{y}=b,\frac{1}{z}=c\Rightarrow a+b+c=0\)
ta xét \(a^3+b^3+c^3-3abc=a^3+b^3+3ab\left(a+b\right)+c^3-3ab-3abc\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b+c\right)=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)
=> \(a^3+b^3+c^3=3abc\) \(\Rightarrow\frac{1}{x^3}+\frac{1}{y^3}+\frac{1}{z^3}=\frac{3}{xyz}\)
=> \(M=\frac{yz}{x^2}+\frac{zx}{y^2}+\frac{xy}{z^2}=\frac{xyz}{x^3}+\frac{xyz}{y^3}+\frac{xyz}{z^3}=xyz\left(\frac{1}{x^3}+\frac{1}{y^3}+\frac{1}{z^3}\right)=xyz.\frac{3}{xyz}=3\)
=> M=3
TM
12 tháng 9 2017
\(M=\frac{yz}{x^2}+\frac{xz}{y^2}+\frac{xy}{z^2}=\frac{y^3z^3+x^3z^3+x^3y^3}{x^2y^2z^2}=\frac{\left(yz+xz\right)^3+x^3y^3-3xy^2z^3-3x^2yz^3}{x^2y^2z^2}\)
\(=\frac{\left(yz+xz+xy\right)\left[\left(yz+xz\right)^2+xy\left(yz+xz\right)+x^2y^2\right]-3xyz^2\left(xz+yz\right)}{x^2y^2z^2}\)
\(=\frac{0.\left[\left(yz+xz\right)^2+xy\left(yz+xz\right)+x^2y^2\right]-3xyz^2\left(xz+yz\right)}{x^2y^2z^2}\)
\(=\frac{-3xyz^2\left(xz+yz\right)}{x^2y^2z^2}=\frac{-3\left(xz+yz\right)}{xy}=\frac{-3.\left(-xy\right)}{xy}=3\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2021
\(A=3yz+\left(4-y-z\right)\left(y+2z\right)\)
\(A=-y^2+4y-2z^2+8z\)
\(A=-\left(y-2\right)^2-2\left(z-2\right)^2+12\le12\)
\(A_{max}=12\) khi \(\left(x;y;z\right)=\left(0;2;2\right)\)
CM
2 tháng 2 2019
Đáp án D
Ta có C 12 1 . C 10 1 = 120
Khi đó C 12 1 . C 10 1 = 120 . Đặt C 12 1 . C 10 1 = 120
Ta luôn có C 12 1 . C 10 1 = 120
C 12 1 . C 10 1 = 120 Suy ra C 12 1 . C 10 1 = 120
Xét hàm số f t = t 2 − 8 t + 3 trên khoảng − 1 ; + ∞ ,có f ' t = 2 t + 1 2 t + 4 t + 3 2 > 0 ; ∀ t > − 1
Hàm số f(t) liên tục trên − 1 ; + ∞ ⇒ f t đồng biến trên − 1 ; + ∞
Do đó, giá trị nhỏ nhất của f(t) là min − 1 ; + ∞ f t = f − 1 = − 3 . Vậy P min = − 3
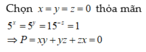
Đề sai? 3^x = 2^y = 12^-x?