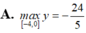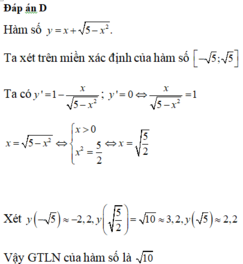Tìm GTLN của hàm số y= x2\(\sqrt{1-x}\) trên (0;1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 12 2021
Bài 1:
\(c,\text{PT có 2 }n_0\text{ phân biệt }\Leftrightarrow\Delta'=2^2-2m>0\Leftrightarrow2m< 4\Leftrightarrow m< 2\)
PT
1
CM
21 tháng 7 2018
Tập xác định R.
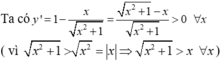
Ta có bảng biến thiên:
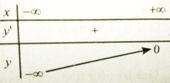
Hàm số không có GTLN trên R . Chọn đáp án C.
DN
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 8 2021
\(y=\dfrac{6\sqrt{2}.x.\dfrac{1}{6\sqrt{2}}+\dfrac{2\sqrt{2}}{3}.\dfrac{3\sqrt{2}}{4}\sqrt{1+9x^2}}{8x^2+1}\)
\(y\le\dfrac{3\sqrt{2}\left(\dfrac{1}{72}+x^2\right)+\dfrac{\sqrt{2}}{3}\left(\dfrac{9}{8}+9x^2+1\right)}{8x^2+1}=\dfrac{\sqrt{2}\left(6x^2+\dfrac{3}{4}\right)}{8x^2+1}\)
\(y\le\dfrac{\dfrac{3\sqrt{2}}{4}\left(8x^2+1\right)}{8x^2+1}=\dfrac{3\sqrt{2}}{4}\)
CM
19 tháng 2 2019
* Hàm số đã cho liên tục trên R vì với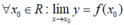 
nên (1) đúng
* Tại điểm x = 0 hàm số không có đạo hàm nên (2) sai.
* y = x 2 - 2 | x | + 2 = | x | 2 - 2 | x | + 2 = ( | x | - 1 ) 2 + 1 ≥ 1 ∀ x
Suy ra, GTNN của hàm số là 1 khi |x| = 1 ⇔ x = ±1
nên hàm số không có GTLN.
* Phương trình x 2 - 2 | x | + 2 = 0 vô nghiệm nên đồ thị không cắt trục hoành.
f ( - x ) = ( - x ) 2 - 2 | - x | + 2 = x 2 - 2 | x | + 2 = f ( x )
Nên hàm số đã cho là hàm số chẵn.
Mệnh đề 1, 5 đúng. Mệnh đề 2, 3,4,6 sai.
Chọn B
TK
0
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 7 2021
24.
\(cos\left(x-\dfrac{\pi}{2}\right)\le1\Rightarrow y\le3.1+1=4\)
\(y_{max}=4\)
26.
\(y=\sqrt{2}cos\left(2x-\dfrac{\pi}{4}\right)\)
Do \(cos\left(2x-\dfrac{\pi}{4}\right)\le1\Rightarrow y\le\sqrt{2}\)
\(y_{max}=\sqrt{2}\)
b.
\(\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{3}+k2\pi\\x-\dfrac{\pi}{6}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
PT
1
