Cho biểu thức A = −x^2−2x−2
b, Chứng minh rằng khi A xác định thì A luôn nhận giá trị âm
c,Tìm GTLN của A
d, Tìm x nguyên để A nhận giá trị nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 1 2023
a: ĐKXĐ: a>=0; a<>4
b: \(M=\dfrac{a\sqrt{a}-a\sqrt{a}+2a-a-2\sqrt{a}}{a-4}=\dfrac{a-2\sqrt{a}}{a-4}=\dfrac{\sqrt{a}}{\sqrt{a}+2}\)
c: Khi a=9 thì \(M=\dfrac{3}{3+2}=\dfrac{3}{5}\)
20 tháng 12 2021
\(a.a\ne\pm1\)
\(b.K=\dfrac{1}{a+1}+\dfrac{2}{a^2-1}=\dfrac{a-1}{\left(a-1\right)\left(a+1\right)}+\dfrac{2}{\left(a-1\right)\left(a+1\right)}=\dfrac{a+1}{\left(a-1\right)\left(a+1\right)}=\dfrac{1}{a-1}\)
\(c.K=\dfrac{1}{1-\dfrac{1}{2}}=\dfrac{1}{\dfrac{1}{2}}=2\)
CM
13 tháng 11 2019
a) Ta có: x - 1 ≠ 0 ⇒ x ≠ 1
x2 - 1 = (x + 1)(x - 1) ≠ 0 ⇔ x ≠ -1 và x ≠ 1
x2 - 2x + 1 = (x - 1)2 ≠ 0 ⇔ x - 1 ≠ 0 ⇔ x ≠ 1
ĐKXĐ: x ≠ -1 và x ≠ 1
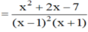
b)Ta có: \(A=-x^2-2x-2\)
\(=-\left(x^2+2x+2\right)=-\left(x+1\right)^2-1\)
Ta có: \(\left(x+1\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x+1\right)^2\le0\forall x\)
\(\Rightarrow-\left(x+1\right)^2-1\le-1\forall x\)
Vì -1 là số âm nên khi giá trị của biểu thức A được xác định thì biểu thức A luôn nhận giá trị âm
c)
Ta có: \(A=-x^2-2x-2\)
\(=-\left(x^2+2x+2\right)=-\left(x+1\right)^2-1\)
Ta có: \(\left(x+1\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x+1\right)^2\le0\forall x\)
\(\Rightarrow-\left(x+1\right)^2-1\le-1\forall x\)
Dấu '=' xảy ra khi
\(-\left(x+1\right)^2=0\Leftrightarrow\left(x+1\right)^2=0\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
Vậy: GTLN của đa thức \(A=-x^2-2x-2\) là -1 khi và chỉ khi x=-1