Cho hình bình hành abcd có A là 50 tính các góc còn lại cải hình bình hành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 12 2022
Câu 10:
góc A=180-130=50 độ
góc B=(180+50)/2=230/2=115 độ
góc C=180-115=65 độ
CM
9 tháng 1 2018
Trong tính chất của hình bình hành:
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
27 tháng 7 2019
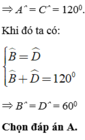
a) Ta thấy : BAD = BCD = 120°( tính chất)
Mà AB//CD ( ABCD là hình bình hành)
=> ABC + BCD = 180°
=> ABC = ADC = 60°
IM
Cho tứ giác ABCD là hình bình hành số đo góc a bằng 120 độ tính số đo góc còn lại của hình bình hành
1
15 tháng 11 2021
Vì ABCD là hbh nên \(\widehat{A}=\widehat{C}=120^0\) và AB//CD
Do đó \(\widehat{B}=\widehat{D}=180^0-\widehat{A}=60^0\) (trong cùng phía)
HT
1
30 tháng 10 2021
\(\widehat{A}=\widehat{C}=135^0\)
\(\widehat{B}=\widehat{D}=45^0\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
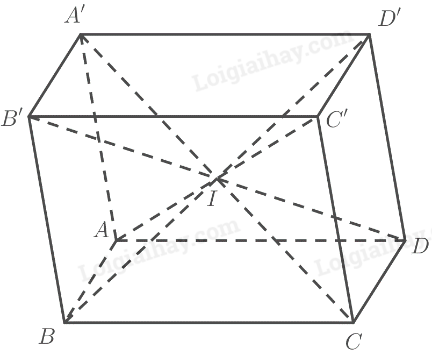
a) Vì \(ABCD.A'B'C'D'\) là hình lăng trụ nên có:
‒ Hai đáy \(ABCD\) và \(A'B'C'D'\) bằng nhau và là hình bình hành.
‒ Các mặt bên \(AA'B'B,AA'D'D,BB'C'C,CC'D'D\) là các hình bình hành.
b) Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {AA'C'C} \right) \cap \left( {ABC{\rm{D}}} \right) = AC\\\left( {AA'C'C} \right) \cap \left( {A'B'C'D'} \right) = A'C'\end{array} \right\} \Rightarrow AC\parallel A'C'\)
Mà \(AA'\) và \(CC'\) là các cạnh bên của hình lăng trụ nên \(AA'\parallel CC'\)
Vậy \(AA'C'C\) là hình bình hành.
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {BB'D'D} \right) \cap \left( {ABC{\rm{D}}} \right) = B{\rm{D}}\\\left( {BB'D'D} \right) \cap \left( {A'B'C'D'} \right) = B'D'\end{array} \right\} \Rightarrow B{\rm{D}}\parallel B'D'\)
Mà \(BB'\) và \(DD'\) là các cạnh bên của hình lăng trụ nên \(BB'\parallel DD'\)
Vậy \(BB'D'D\) là hình bình hành.
c) Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right) = C{\rm{D}}\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {A'B'C'D'} \right) = A'B'\end{array} \right\} \Rightarrow C{\rm{D}}\parallel A'B'\left( 1 \right)\)
\(ABC{\rm{D}}\) là hình bình hành nên \(AB = CD\)
\(AA'B'B\) là hình bình hành nên \(AB = A'B'\)
Vậy \(A'B' = CD\left( 2 \right)\)
Từ (1) và (2) suy ra \(A'B'C{\rm{D}}\) là hình bình hành
\( \Rightarrow A'C,B'D\) cắt nhau tại trung điểm của mỗi đường.
Chứng minh tương tự ta có:
+ \(ABC'D'\) là hình bình hành nên \(AC',B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường
+ \(A'BCD'\) là hình bình hành nên \(A'C,B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường
Do đó bốn đoạn thẳng \(A'C,AC',B'D,BD\) có cùng trung điểm.
CM
17 tháng 6 2017
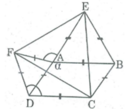
Vì ∠ (BAD) + ∠ (BAE) + ∠ (EAF) + ∠ (FAD) = 360 0
⇒ ∠ (EAF) = 360 0 – ( ∠ (BAD) + ∠ (BAE) + ∠ (FAD) )
Mà ∠ (BAD) = α 2 (gt)
∠ (BAE) = 60 0 (ΔBAE đều)
∠ (FAD) = 60 0 (ΔFAD đều)
Nên ∠ (EAF) = 360 0 – ( α 2 + 60 0 + 60 0 ) = 240 0 – α
10 tháng 8 2023
a: Xét ΔMEA và ΔMCB có
góc EMA=góc CMB
MA=MB
góc MEA=góc MCB
=>ΔMEA=ΔMCB
=>ME=MC
=>M là trung điểm của CE
Xét tứ giác AEBC có
M là trung điểm chung của AB và EC
=>AEBC là hbh
b: Để AEBC là hình chữ nhật thì góc EAC=90 độ
=>góc DAC=90 độ
=>góc ACD+góc D=90 độ
mà góc ACD=1/2*góc D
nên góc D=2/3*90=60 độ
=>góc B=60 độ
góc BAD=góc BCD=180-60=120 độ
Ta có:
\(\widehat{A}=\widehat{C}=50^o\)
\(\widehat{B}=\widehat{C}=130^o\)
nhanh lên