Cho (d) có phương trình y=(2k-1)x k-2(k là than số) . Câu1: tìm k để (d) // (d

ON

Omega Neo

25 tháng 11 2019

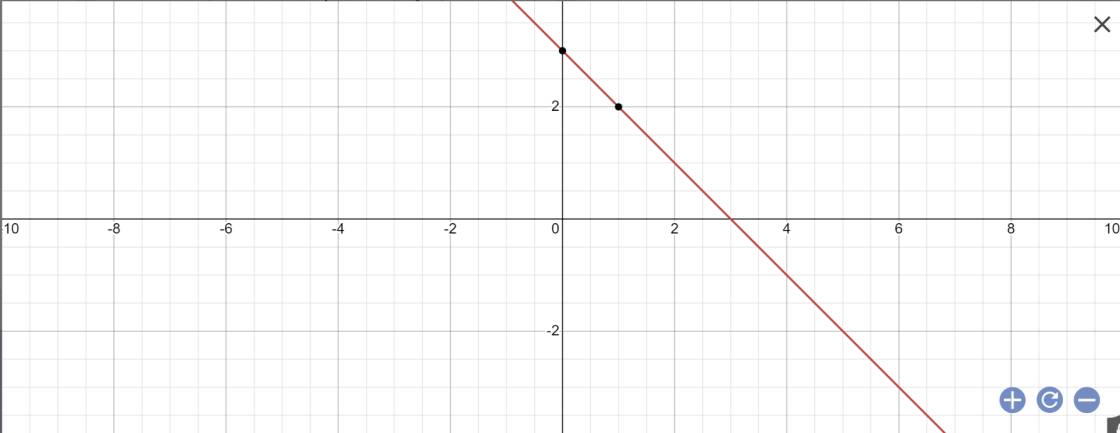
Cho (d) có phương trình y=(2k-1)x+k-2(k là than số) . Câu1: tìm k để (d) // (d') có phương trình y= -3x +5 Câu2: Với k tìm được ở câu a. Vẽ (d) và tính khoảng cách từ D(0;0) đến (d). Câu3: Tìm điểm cố định mà (d) luôn đi qua mọi k. Câu4: Tìm k để khoảng cách từ D(0;0) đến (d) là lớn nhất. Giải hộ...

Đọc tiếp

#Toán lớp 9

0

HN

Hoàng Ngọc Quỳnh Anh

4 tháng 1

cho hàm số y= -x = 3 (d)

a, Vẽ

b, tìm k để y = ( 2k - 1 ) x + 1 song song (d)

c, tìm k để y = ( k - 3) x + 5 cắt (d)

tại điểm có trung độ = 7

#Toán lớp 8

2

AH

Akai Haruma

Giáo viên

4 tháng 1

Lời giải:

** Sửa lại hàm số: $y=-x+3$

a. Bạn có thể tự vẽ.

b. Để $y=(2k-1)x+1$ song song với (d)$ thì:

$2k-1=-1$

$\Leftrightarrow k=0$

c. PT hoành độ giao điểm của $(d)$ và $y=(k-3)x+5$:

$-x+3=(k-3)x+5$

$\Leftrightarrow (k-2)x=-2$

$\Leftrightarrow x=\frac{-2}{k-2}$ (đk: $k\neq 2$)

Khi đó: $y=-x+3=\frac{2}{k-2}+3$

Hai đths cắt nhau tại điểm có tung độ $7$

$\Leftrightarrow \frac{2}{k-2}+3=7$

$\Leftrightarrow \frac{2}{k-2}=4$

$\Leftrightarrow k-2=\frac{1}{2}\Leftrightarrow k=2,5$

Đúng(1)

NL

Nguyễn Lê Phước Thịnh

4 tháng 1

a: Sửa đề: y=-x+3

Vẽ đồ thị

loading...

b: Để đường thẳng y=(2k-1)x+1 song song với (d) thì

$\left\{{}\begin{matrix}2k-1=-1\\1\ne3\left(đúng\right)\end{matrix}\right.$

=>2k-1=-1

=>2k=0

=>k=0

c: Thay y=7 vào y=-x+3, ta được:

-x+3=7

=>-x=4

=>x=-2

Thay x=-2 và y=7 vào y=(k-3)x+5, ta được:

-2(k-3)+5=7

=>-2(k-3)=2

=>k-3=-1

=>k=2

Đúng(0)

HH

Hồng Hạnh

4 tháng 11 2015 - olm

Cho hàm số y=(2k-1)x+k (d)
a, Tìm k để đường thẳng (d) đi qua gốc tọa độ
b, Tìm k để đường thẳng (d) cắt trục hoành tại điểm có hoành độ = 3
c, Tìm k để đường thẳng (d) song song với đường thẳng y= 3/5x+4
d, Tìm k để điểm M (-3;2) thuộc đồ thị hàm số đã cho

#Toán lớp 9

1

NT

Nguyễn Thị Thùy Dương

4 tháng 11 2015

a, b=k=0

b,(2k-1).3+k=0 => 3k=3 => k =1

c, 2k-1 = 3/5=> 2k = 8/5 => k = 4/5 khác 4 vậy k = 4/5

d, (2k-1)(-3) +k =2 => -5k =-1 => k =1/5

Đúng(0)

NN

nguyen ngoc son

5 tháng 2 2022

Cho phương trình x² – 2(k + 2)x + k² + 2k – 7 = 0 (m là tham số)

a) Giải phương trình khi k = - 3

b) Tìm k để phương trình có nghiệm x₁; x₂ thỏa mãn $x_1^2+x_2^2=x_1x_2+28$

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

5 tháng 2 2022

a: Thay k=-3 vào pt, ta được:

$x^2-2\cdot\left(-3+2\right)x+\left(-3\right)^2+2\cdot\left(-3\right)-7=0$

$\Leftrightarrow x^2+2x-4=0$

$\Leftrightarrow\left(x+1\right)^2=5$

hay $x\in\left\{\sqrt{5}-1;-\sqrt{5}-1\right\}$

b: $\text{Δ}=\left(2k+4\right)^2-4\left(k^2+2k-7\right)$

$=4k^2+16k+16-4k^2-8k+28$

=8k+44

Để phương trình có hai nghiệm thì 8k+44>=0

=>8k>=-44

hay k>=-11/2

Theo đề, ta có: $\left(x_1+x_2\right)^2-3x_1x_2=28$

$\Leftrightarrow\left(2k+4\right)^2-3\cdot\left(k^2+2k-7\right)=28$

$\Leftrightarrow4k^2+16k+16-3k^2-6k+21=28$

$\Leftrightarrow k^2+10k+37-28=0$

$\Leftrightarrow\left(k+1\right)\left(k+9\right)=0$

=>k=-1

Đúng(2)

PT

Phan Thị Ngọc Gìau

4 tháng 4 2017 - olm

Trên mặt phẳng toạ độ cho đường thẳng (d) có phương trình: 2kx + (k – 1)y = 2 (k là tham số)

1. Tìm k để đường thẳng (d) song song với đường thẳng y = ? Khi đó hãy tính góc tạo bởi (d) và tia Ox.

2. Tìm k để khoảng cách từ gốc toạ độ đến đường thẳng (d) là lớn nhất?

#Toán lớp 9

0

BC

Bui Cam Lan Bui

30 tháng 9 2015 - olm

Trên mặt phẳng toạ độ cho đường thẳng (d) có phương trình: 2kx + (k – 1)y = 2 (k là tham số)

1. Tìm k để đường thẳng (d) song song với đường thẳng y = ? Khi đó hãy tính góc tạo bởi (d) và tia Ox.

2. Tìm k để khoảng cách từ gốc toạ độ đến đường thẳng (d) là lớn nhất?

#Toán lớp 9

1

DD

Đinh Đức Tài

30 tháng 9 2015

^o---^o

Đúng(0)

NN

nguyen ngoc son

6 tháng 2 2022

Cho phương trình x² – 2(k + 2)x + k² + 2k – 7 = 0 (m là tham số)

Tìm k để phương trình có nghiệm x₁; x₂ thỏa mãn$x_1^2+x_2^2=x_1x_2+28$

#Toán lớp 9

1

NT

Nguyễn Thanh Hằng

6 tháng 2 2022

Xét pt :

$x^2-2\left(k+2\right)x+k^2+2k-7=0$

$\Delta'=\left(k+2\right)^2-\left(k^2+2k-7\right)$

$=k^2+4k+4-k^2-2k+7$

$=2k+11$

Để phương trình có 2 nghiệm pb $\Leftrightarrow k>-\dfrac{11}{2}$

Theo định lí Viet ta có :

$\left\{{}\begin{matrix}x_1+x_2=2\left(k+2\right)\\x_1.x_2=k^2+2k-7\end{matrix}\right.$

Ta có :

$x_1^2+x_2^2=x_1.x_2+28$

$\Leftrightarrow\left(x_1+x_2\right)^2=3x_1.x_2+28$

$\Leftrightarrow4\left(k+2\right)^2=3\left(k^2+2k-7\right)+28$

Tự giải hết pt tìm k nhé :> Buồn ngủ quá ~

Đúng(2)

HQ

Hồ Quốc Khánh

1 tháng 1 2016 - olm

Tìm k để 3 đường thẳng sau đồng quy : (d₁) : x - y + 5k = 0; (d₂) : (2k + 3)x + k(y - 1) = 0; (d₃) : (k + 1)x - y + 1 = 0.

#Toán lớp 9

3

B

bích

1 tháng 1 2016

tik mik nha mik tik lại

câu hỏi này mik chưa học đến vì mik mới học lớp 6 thui

Đúng(0)

TT

Trần Trương Quỳnh Hoa

1 tháng 1 2016

tham khảo chtt nha bạn

chứ câu này mk chưa có học

Đúng(0)

HN

Huong Nguyen

27 tháng 5 2016 - olm

rên mặt phẳng tọa độ cho đường thẳng (d) có phương trình : 2kx + (k – 1)y = 2 (k là tham số) a) Với giá trị nào của k thì đường thẳng (d) song song với đường thẳng y=x$\sqrt{3}$ b) Tìm k để khoảng cách từ gốc tọa độ đến (d) là lớn nhất.

#Toán lớp 9

0