Một chất điểm cân bằng dưới tác dụng của 3 lực đồng phẳng F1 = 10N, F2 = 20√3 N, góc tạo bởi F1 và F2 60 độ. Tìm độ lớn của F3 và góc tạo bởi hướng của F3 vs F1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
23 tháng 3 2017
Đáp án là A
Điều kiện cân bằng:
F 1 → + F 2 → + F 3 → = 0 → → - F 2 → = F 1 → + F 3 → . (1)
- Bình phương vô hướng 2 vế của (1):
F 2 2 = F 1 2 + F 3 2 + 2 F 1 F 3 . cosα → 36 = F 1 2 + F 3 2 + 2 F 1 F 3 . cos 60 0 .
→ F 1 2 - F 1 F 3 + ( F 3 2 - 36 ) = 0 ( 2 ) ; ∆ = F 3 2 - 4 ( F 3 2 - 36 ) .
- Để phương trình (1) có nghiệm thì:
∆ ≥ 0 → F 3 2 - 4 ( F 3 2 - 36 ) ≥ 0 → 0 < F 3 ≤ 4 3 = 6 , 9 .
VT
29 tháng 3 2018
Chọn A.
Điều kiện cân bằng:
F 1 → + F 2 → + F 3 → = 0 → ⇒ - F 3 → = F 1 → + F 2 → .
Bình phương vô hướng hai vế:
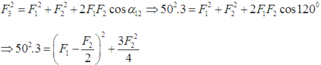
Muốn F2 lớn nhất
VT
18 tháng 3 2018
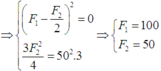
Đáp án D
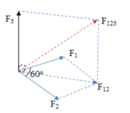
Hợp lực của F1 và F2 là:
F 12 = 2. F 1 . cos α 2 = 2.20. cos 30 0 = 20 3 N
F3 vuông góc với mp chứa F1 và F2 nên F3 vuông góc với F12.
Hợp lực của ba lực chính là hợp lực của F12 và F3.
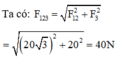
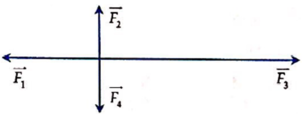
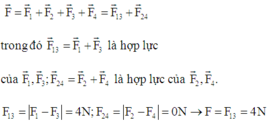
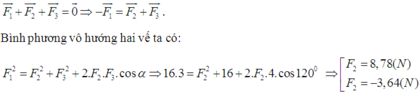
Vì vật đứng yên nên độ lớn của hợp lực F1 và F2 sẽ bằng độ lớn của F3
\(F_{12}=\sqrt{F_1^2+F_2^2+2F_1F_2\cos\left(F_1;F_2\right)}=\sqrt{100+1200+2.10.20\sqrt{3}.\frac{1}{2}}\approx40,6\left(N\right)\)
\(\Rightarrow F_3=40,6\left(N\right)\)
\(F_2^2=F_1^2+F_3^2+2F_1F_3\cos\left(F_1;F_3\right)\)
Tất cả dữ kiện đều đã có, bạn tự áp dụng vào để tính góc tạo bởi F1 và F3