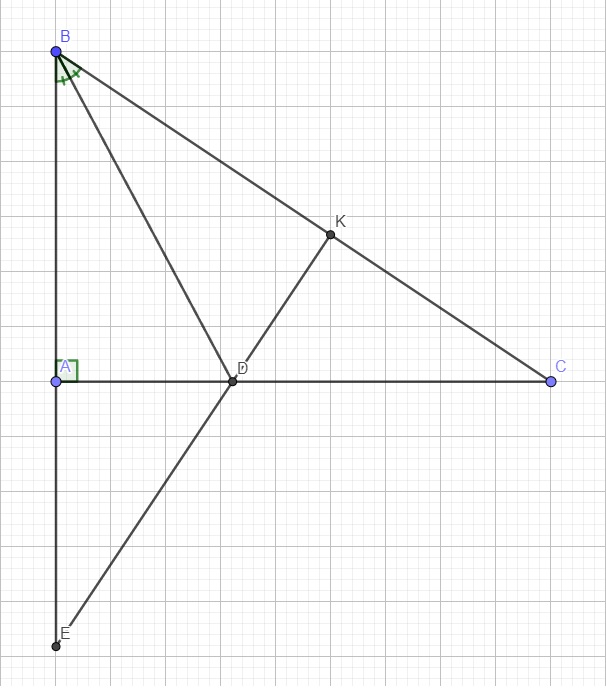
Cho /\ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D. Vẽ DK vuông BC tại K.
A) CM:/\BAD =/\BKD và AD =KD.
B) Trên tia đối của tia AB lấy điểm E sao cho BE =BC. Tia BD cắt EC tại H. CM:BH vuông với EC
C) CM : K, D, E thẳng hàng.
Giúp mk với >_<

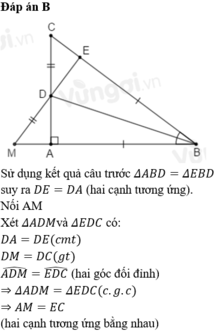
a) Tính BC:
Ta có: Aˆ=90oA^=90o (ΔABC vuông tại A) {o là độ}
Áp dụng định lí PITAGO đối với ΔABC:
Ta có: BC2 = AB2 + AC2
=> BC2 = 62 + 82
=> BC2 = 100
=> BC =100−−−√=10(cm)100=10(cm)
b) ΔABK là tam giác...:
Ta có:
BK (BD) là đường phân giác của góc B (1)
AE vuông góc với BK (BD)
=> BK là đường vuông góc (2)
Từ (1) và (2):
=> ABK là tam giác cân (vì tam giác có đường phân giác đồng thời là đường cao là tam giác cân)
c) DK ⊥ BC:
Vì ΔKED vuông tại E (do AE ⊥ BD)
Ta có: E=90o⇒EKDˆ+KDEˆ=90oE=90o⇒EKD^+KDE^=90o
Áp dụng tính chất góc ngoài của tam giác bằng tổng hai góc trong không kề với nó:
⇒DKCˆ=EKDˆ+KDEˆ=90o
hay DK ⊥ BC.