Giúp em câu 9 ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SN
2
giúp em câu 8 câu 9 với em cần gấp ạ
H
22 tháng 7 2021
Câu 9 :
a) $FeO + H_2SO_4 \to FeSO_4 + H_2O$
$n_{FeSO_4} =n_{H_2SO_4} = n_{FeO} = \dfrac{7,2}{72} = 0,1(mol)$
$m_{dd\ H_2SO_4} = \dfrac{0,1.98}{24,5\%} = 40(gam)$
$m_{dd\ sau\ pư} = 40 + 7,2 = 47,2(gam)$
Gọi $n_{FeSO_4.7H_2O} = a(mol)$
Sau khi tách :
$m_{dd} = 47,2 - 278a(gam)$
$n_{FeSO_4} = 0,1 - a(mol)$
Suy ra :
$C\% = \dfrac{152(0,1 - a)}{47,2 - 278a}.100\% = 12,18\%$
$\Rightarrow a = 0,08$
$m = 0,08.278 =22,24(gam)$
29 tháng 6 2023
3:
\(=\dfrac{2}{1+cotx-tanx-1}=\dfrac{2}{cotx-tanx}\)
\(=2:\left(\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}\right)=2:\dfrac{cos^2x-sin^2x}{sinx\cdot cosx}\)
\(=\dfrac{sin2x}{cos2x}\)
=tan2x
4:
\(=\left(1-\dfrac{1}{cot^2x}\right)\cdot cotx=cotx-\dfrac{1}{cotx}=\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}\)
\(=\dfrac{cos^2x-sin^2x}{sinx\cdot cosx}=\dfrac{cos2x}{\dfrac{1}{2}\cdot2\cdot sinx\cdot cosx}=\dfrac{cos2x}{sin2x}\cdot2\)
6:
\(=\dfrac{\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}}{cos2x}=\dfrac{cos^2x-sin^2x}{sinx\cdot cosx}:cos2x=\dfrac{1}{sinx\cdot cosx}\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2022
9.
Gọi D là trung điểm BC \(\Rightarrow AD\perp BC\) (do tam giác ABC đều)
Mặt khác \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
\(\Rightarrow BC\perp\left(SAD\right)\)
Mà BC là giao tuyến (SAB) và (SBC)
\(\Rightarrow\widehat{SDA}\) là góc giữa (ABC) và (SBC)
\(AD=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow tan\widehat{SDA}=\dfrac{SA}{AD}=\dfrac{1}{\sqrt{3}}\)
\(\Rightarrow\widehat{SDA}=30^0\)
b.
Câu b nhìn không rõ, đề yêu cầu tính diện tích tam giác SBC đúng không nhỉ?
Từ câu a ta có \(BC\perp\left(SAD\right)\Rightarrow SD\perp BC\)
Pitago tam giác SAD: \(SD=\sqrt{SA^2+AD^2}=a\)
\(\Rightarrow S_{\Delta SBC}=\dfrac{1}{2}SD.BC=\dfrac{a^2}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2023
Đặt \(z=x+yi\)
\(\Rightarrow\left(2-i\right)\left(x-yi\right)+\left(4+3i\right)\left(x+yi\right)=7-4i\)
\(\Leftrightarrow2x-y-\left(x+2y\right)i+4x-3y+\left(3x+4y\right)i=7-4i\)
\(\Leftrightarrow6x-4y+\left(2x+2y\right)i=7-4i\)
\(\Rightarrow\left\{{}\begin{matrix}6x-4y=7\\2x+2y=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{10}\\y=-\dfrac{19}{10}\end{matrix}\right.\)
\(\Rightarrow z=-\dfrac{1}{10}-\dfrac{19}{10}i\)
27 tháng 10 2021
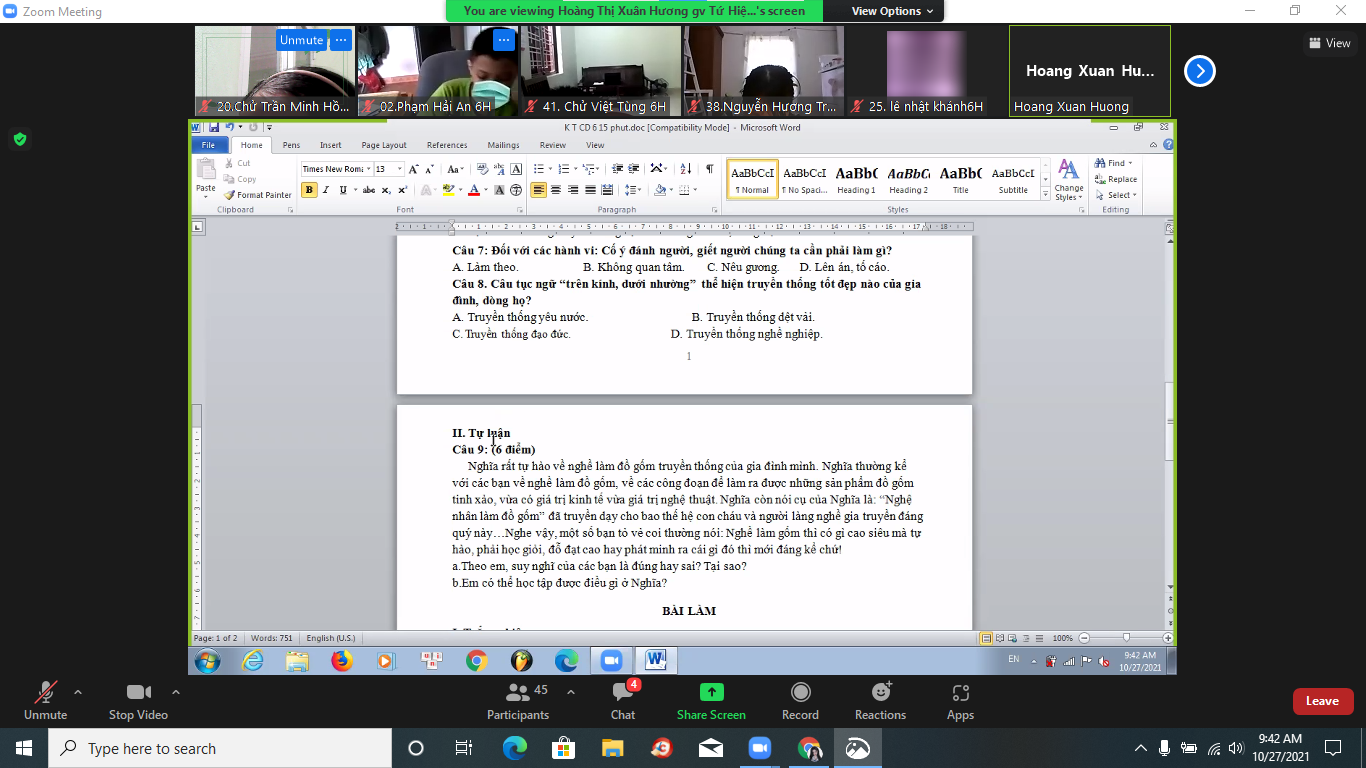
a/ Theo em, suy nghĩ của các bạn là sai
- Giải thích:
+ Vì mỗi chúng ta cần phải biết tự hào về truyền thống của gia đình dòng họ của mình.
+ Đó là những giá trị tốt đẹp cần được giữ gìn và phát huy , những truyền thống đó giúp chúng ta có thêm sức mạnh, kinh nghiệm trong cuộc sống.
b/ Học tập bạn Nghĩa: Phải trân trọng tự hào, giữ gìn truyền thống gia đình
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 5 2021
\(log_3\left(\dfrac{a^4}{9}\right)=log_3a^4-log_39=4log_3a-2=2\left(2log_3-1\right)\)
26 tháng 10 2021
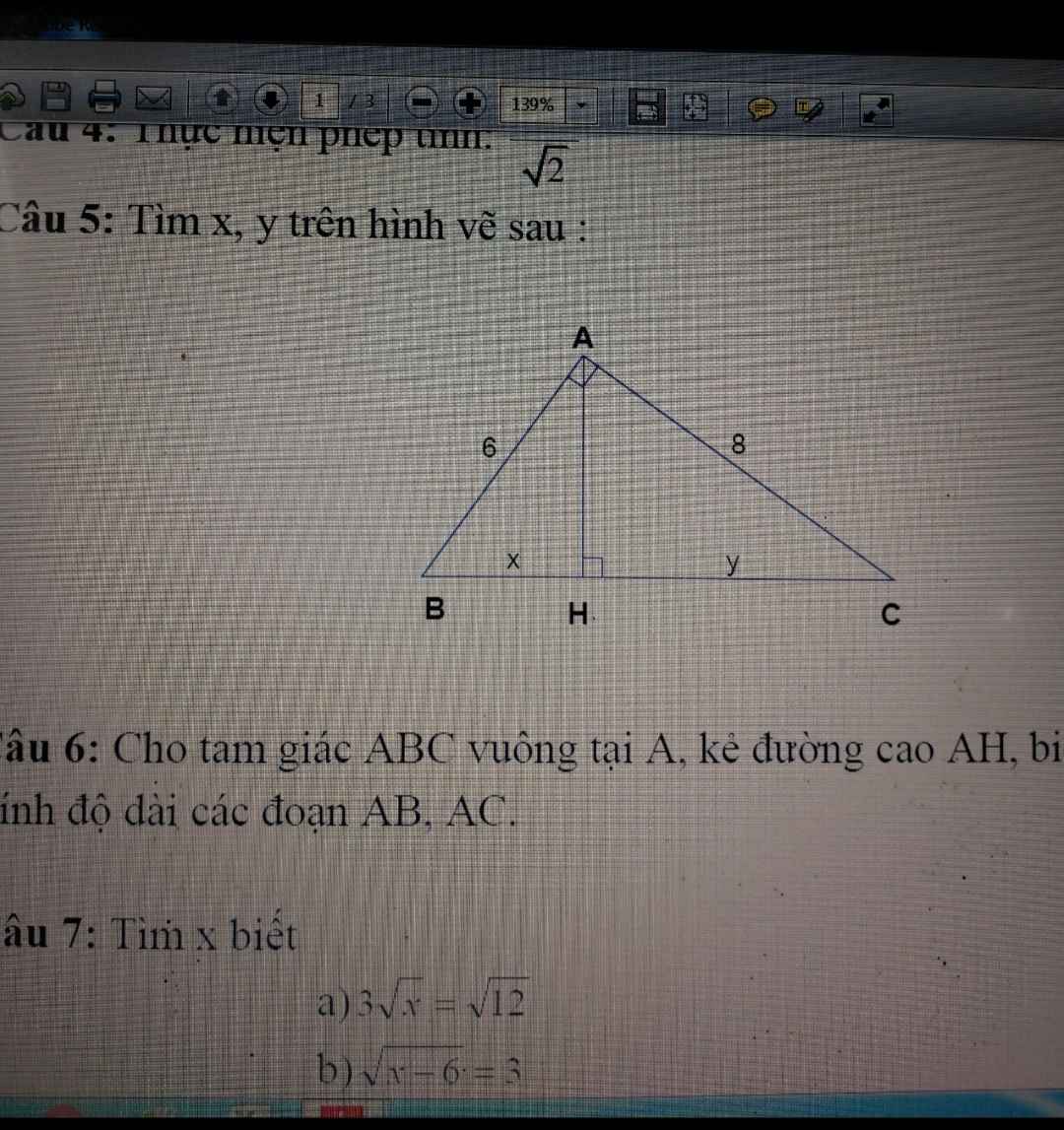
câu 5:
x=3,6
y=6,4
câu 6: chụp lại đề
câu 7:
a)ĐKXĐ: \(x\ge0\)
\(3\sqrt{x}=\sqrt{12}\\ \Rightarrow9x=12\\ \Rightarrow x=\dfrac{4}{3}\)
b) ĐKXĐ: \(x\ge6\)
\(\sqrt{x-6}=3\\ \Rightarrow x-6=9\\ \Rightarrow x=15\)
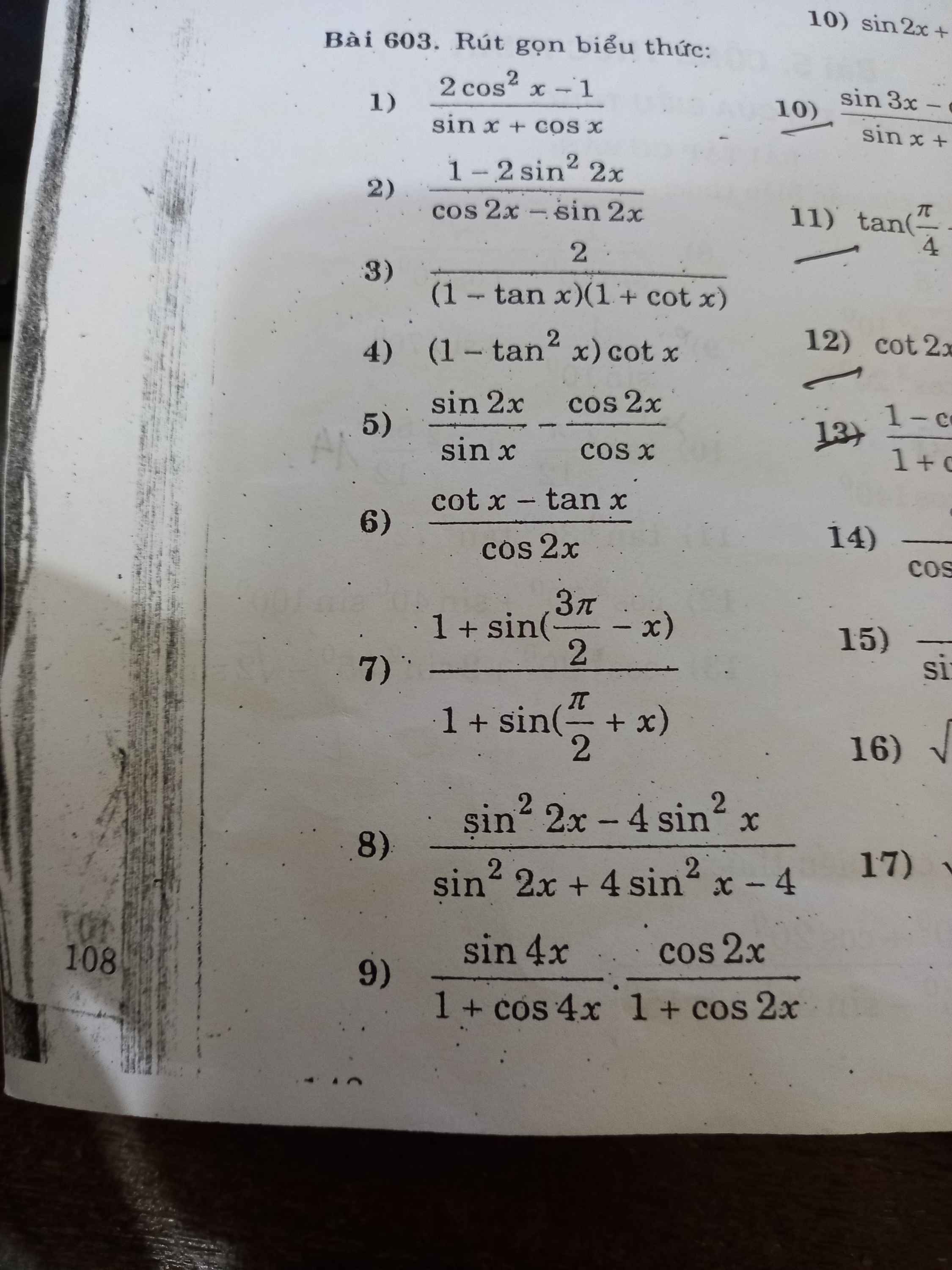
\(24p=0,4h\)
Tốc độ tb của học sinh đó khi đi từ nhà đến trường:
\(v=s:t=2,16:0,4=5,4\)km/h = 1,5m/s
\(\Rightarrow ChonB\)
1,5m/s