1) Cho tam giác ABC, B = 60o, BC = 8cm; AB + AC = 12cm. Tính độ dài cạnh AB.
2) Cho đa thức bậc bốn f(x) có hệ số bậc cao nhất bằng 1 và f(1) = 10, f(2) = 20 và f(3) = 30. Tính f(10) + f(-6)
Làm được đến đâu thì làm nhé. Ai nhanh và đúng thì mình sẽ tick và add friends nhé. Thanks. Please help me!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
MH
3 tháng 2 2021
Dựng \(AH\) vuông góc \(BC\). Đặt \(AB=x\Rightarrow AH=x.\sin60^0=\dfrac{x\sqrt{3}}{2};BH=x\cos60^0=\dfrac{x}{2}\)
\(\Rightarrow HC=BC-BH=8-\dfrac{x}{2};AC=12-x\)
Tam giác \(AHC\) vuông tại \(H\Rightarrow AC^2=AH^2+HC^2\Rightarrow\left(12-x\right)^2=\dfrac{3x^2}{4}+\left(8-\dfrac{x}{2}\right)^2\)
Giải phương trình trên ta được \(x=5\).
Vậy \(AB=5cm\).
11 tháng 2 2021
a) Xét ΔABC có
BA<BC(gt)
mà góc đối diện với cạnh BA là \(\widehat{ACB}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{BAC}>\widehat{ACB}\)(Quan hệ giữa cạnh và góc đối diện trong tam giác)
b) Xét ΔABH vuông tại H và ΔAMH vuông tại H có
HB=HM(gt)
AH chung
Do đó: ΔABH=ΔAMH(hai cạnh góc vuông)
Suy ra: BA=MA(hai cạnh tương ứng)
Xét ΔBAM có BA=MA(cmt)
nên ΔBAM cân tại A(Định nghĩa tam giác cân)
Xét ΔBAM cân tại A có \(\widehat{B}=60^0\)(gt)
nên ΔBAM đều(Dấu hiệu nhận biết tam giác đều)
CM
22 tháng 12 2017
Áp dụng định lý Sin trong tam giác ABC ta có:
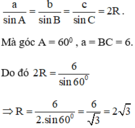
Vậy bán kính đường tròn ngoại tiếp tam giác bằng 2√3.
18 tháng 9 2021
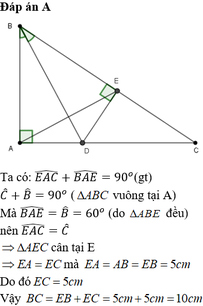
Trên BC lấy điểm E sao cho \(AB=BE\)
Dễ dàng chứng minh được \(\Delta ABD=\Delta EBD\left(c.g.c\right)\)
Do đó \(\widehat{BAC}=\widehat{BED}=80^0\)
Mà \(\widehat{BED}\) là góc ngoài tam giác DEC
\(\Rightarrow\widehat{BED}=\widehat{EDC}+\widehat{BCA}\\ \Rightarrow80^0=\widehat{EDC}+40^0\\ \Rightarrow\widehat{EDC}=40^0\Rightarrow\widehat{EDC}=\widehat{ECD}\left(=40^0\right)\\ \Rightarrow\Delta EDC.cân.tại.E\Rightarrow DE=EC\)
Vậy \(AB+AD=BE+EC=BC\)
6 tháng 4 2022
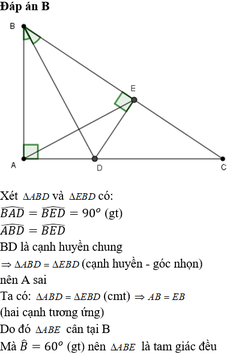
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên BA=BE
hay ΔBAE cân tại B
mà \(\widehat{ABE}=60^0\)
nên ΔBAE đều
