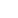
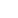
Xác định bậc, hệ số tự do, hệ số cao nhất, của đa thứcP(x)= Đáp án: Bậc của đa thức là: Trả lời Hệ số tự do của đa thức là: Trả lời Hệ số cao nhất của đa thức là:

TD

Trương Dung Dung

15 tháng 10 2021

Xác định bậc, hệ số tự do, hệ số cao nhất, của đa thứcP(x)= Đáp án: Bậc của đa thức là: Trả lời Hệ số tự do của đa thức là: Trả lời Hệ số cao nhất của đa thức...

Đọc tiếp

#Toán lớp 7

0

PN

phạm nguyễn huy nhật

16 tháng 3 2022

Tìm bậc, hệ số cao nhất, hệ số tự do của đa thức một biến sau:

3x^{5}+3x^{4}-2x^{3}x^{3}+73x5+3x4−2x3x3+7

Đáp số:

Bậc của đa thức là:

Hệ số cao nhất:

Hệ số tự do:

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

29 tháng 1

$3x^5+3x^4-2x^3+7$

bậc là 5

Hệ số cao nhất là 3

Hệ số tự do là 7

Đúng(0)

S

subjects

10 tháng 1 2023 - olm

câu 1 : tìm bậc, hệ số cao nhất và hệ số tự do của đa thức : $P=-x^3-2x^2+x^3+4x+5$ câu 2 xác định bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức sau : a) $5x^2-2x+1-3x^4$ b) $1,5x^2-3,4x^4+0,5x^2-1$ câu 3 : a) Tính $\left(\dfrac{1}{2}x^3\right)\times\left(-4x^2\right)$. tìm hệ số và bậc của đơn thức nhận được b) Tính $\dfrac{1}{2}x^3-\dfrac{5}{2}x^3$. tìm hệ số và bậc của đơn thức nhận được câu...

Đọc tiếp

câu 1 : tìm bậc, hệ số cao nhất và hệ số tự do của đa thức : $P=-x^3-2x^2+x^3+4x+5$

câu 2 xác định bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức sau :

a) $5x^2-2x+1-3x^4$

b) $1,5x^2-3,4x^4+0,5x^2-1$

câu 3 :

a) Tính $\left(\dfrac{1}{2}x^3\right)\times\left(-4x^2\right)$. tìm hệ số và bậc của đơn thức nhận được

b) Tính $\dfrac{1}{2}x^3-\dfrac{5}{2}x^3$. tìm hệ số và bậc của đơn thức nhận được

câu 4 : cho 2 đa thức :

$A\left(x\right)=x^3+\dfrac{3}{2}x-7x^4+\dfrac{1}{2}x-4x^2+9$ và $B\left(x\right)=x^5-3x^2+8x^4-5x^2-x^5+x-7$

a) thu gọn và sắp xếp 2 đa thức trên theo lũy thừa giảm của biến

b) tìm bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức đã cho

câu 5 : cho 2 đa thức :

$P\left(x\right)=5x^3+2x^4-x^2+3x^2-x^3-2x^4-4x^3$ và

$Q\left(x\right)=3x-4x^3+8x^2-5x+4x^3+5$

thu gọn và sắp xếp 2 đa thức trên theo lũy thừa giảm của biến

câu 6 : người ta dùng 2 máy bơm để bơm nước vào bể chứa nước. máy thứ nhất bơm mỗi giờ được $22m^3$ nước. máy thứ 2 bơm mỗi giờ được $16m^3$ nước. sau cả hai máy chạy trong $x$ giờ, người ta tắt máy thứ nhất và để máy thứ 2 chạy thêm $0,5$ giờ nữa thì bể nước đầy.

hãy viết đa thức (biến $x$) biểu thị dung tích của mỗi bể ($m^3$), biết rằng trước khi bơm trong bể có $1,5m^3$ nước. tìm hệ số cao nhất và hệ số tự do của đa thức đó.

câu 7 : viết đa thức $F\left(x\right)$ thỏa mãn đồng thời các điều kiện sau :

$\cdot$ bật của $F\left(x\right)$ bằng $3$

$\cdot$ hệ số của $x^2$ bằng hệ số của $x$ và bằng $2$

$\cdot$ hệ số cao nhất của $F\left(x\right)$ bằng $-6$ và hệ số tự do bằng $3$

câu 8 : kiểm tra câu hỏi sau :

a) $x=\dfrac{-1}{8}$ có phải là nghiệm của đa thức $P\left(x\right)=4x+\dfrac{1}{2}$ không

b) trong 3 số $1;-1;2$, số nào là số nghiệm của đa thức $Q\left(x\right)=x^2+x-2?$

câu 9 : mẹ cho quỳnh 100 000 đồng. quỳnh mua một bộ dụng cụ học tập có giá 37 000 đồng và một cuốn sách tham khảo môn toán với giá $x$ (nghìn đồng).

a) hãy tìm đa thức (biến $x$) biểu thị số tiền quỳnh còn lại (đơn vị nghìn đồng). tìm bậc của đa thức đó.

b) sau khi mua sách thì quỳnh tiêu vừa hết số tiền mẹ cho, hỏi số tiền của cuốn sách là bao nhiêu ?

#Toán lớp 7

1

CT

Cô Tuyết Ngọc

Manager VIP

10 tháng 1 2023

Em muốn hỏi bài nào vậy? Quá nhiều bài thầy cô và các bạn không thể trả lời được hết em ạ

Đúng(1)

DT

Đinh Thu Trang

16 tháng 4 2023

loading... giúp em bài 4 với ạ

Đúng(0)

AH

ai Huy là

8 tháng 5 2020

Xác định bậc của đa thức ,hệ số cao nhất, hệ số tự do của đa thức:5x^2-3x+4

#Toán lớp 7

2

AH

Akai Haruma

Giáo viên

8 tháng 5 2020

Lời giải:

Bậc của đa thức là bậc của của hạng tử có số mũ lớn nhất trong dạng thu gọn của đa thức đó. Ở đây ta thấy đa thức đã thu gọn rồi và có số mũ $2$ trong $x^2$ là cao nhất nên bậc của đa thức là $2$

Hệ số cao nhất gắn liền với biến có số mũ cao nhất. Ở đây hệ số cao nhất là 5

Hệ số tự do là hệ số không gắn với biến (biến mũ 0) và là $4$

Đúng(1)

NT

Nguyễn Thanh Hải

9 tháng 5 2020

Bậc của đa thức là 2

Hệ số cao nhất là 5

Hệ số tự do là 4

Nhớ tick cho mình nha!

Đúng(1)

H

Huyền

3 tháng 4 2018 - olm

xác định đa thức 1 biến f(x) biết đa hức f(x) có bậc 2 ,hệ số cao nhất là 1 hệ số tự do là 9 nghiệmcủa đa thức f(x) là 3
GIUP MIK VS,CẢM ƠN!

#Toán lớp 7

0

TT

tiểu Tiêu yêu rainbow_xumengje

26 tháng 11 2023

Cho đa thức bậc 5 một biến có hai hạng tử mà hệ số cao nhất là 2 và hệ số tự do là 64. Nghiệm của đa thức này là...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

26 tháng 11 2023

Gọi A là đa thức cần tìm

Đa thức bậc năm một biến có hai hạng tử mà hệ số cao nhất là 2 nên Đa thức chắc chắn sẽ có dạng là $A=2x^5+B$

Hệ số tự do là 64 mà đa thức A chỉ có hai hạng tử nên $A=2x^5+64$

Đặt A=0
=>$2x^5+64=0$

=>$x^5+32=0$

=>$x^5=-32$

=>x=-2

Đúng(0)

LL

linh linh li

14 tháng 8 2021

Cho hai đa thức biến x : A = ax^2 - 3x - 18 và B = 1 + 4x - 7x^2

a) Xác định bậc , hệ số cao nhất , hệ số tự do của B

b) Xác định hệ số a xuất hiện ở đa thức A , biết rằng A có một nghiệm là 2

c) Với a tìm được . tìm đa thức C sao cho C + B = A

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 8 2021

a: Bậc là 2

Hệ số cao nhất là -7

Hệ số tự do là 1

b: Thay x=2 vào A=0, ta được:

$a\cdot2^2-3\cdot2-18=0$

$\Leftrightarrow4a=24$

hay a=6

c: Ta có: C+B=A

nên C=A-B

$=6x^2-3x-18-1-4x+7x^2$

$=13x^2-7x-19$

Đúng(1)

TH

Thanh Hằng Trần

25 tháng 2 2018 - olm

a)tìm nghiệm của đa thức 2x-6;2x^2-4x; x^2+4

b) tìm một đa thức một biến không có nghiệm

c) tìm một đa thức một biến bậc 4 có hệ số cao nhất là -4, hệ số tự do là 3, hệ số bậc hai là -1

#Toán lớp 7

0

TT

Tùng Trương Quang

VIP

22 tháng 7 2023

Tìm đa thức P(x) bậc 3 thõa mãn các điều kiện sau:- P(x) khuyết hạng tử bậc 2- Hệ số cao nhất là 4- Hệ số tự do là 0- x = $\dfrac{1}{2}$ là 1 nghiệm của đa thức...

Đọc tiếp

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

22 tháng 7 2023

P(x)=ax^3+bx+c

Hệ số cao nhất là 4 nên a=4

=>P(x)=4x^3+bx+c

Hệ số tự do là 0 nên P(x)=4x^3+bx

P(1/2)=0

=>4*1/8+b*1/2=0

=>b=-1

=>P(x)=4x^3-x

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

17 tháng 9 2023

Viết đa thức trong mỗi trường hợp sau:

a) Đa thức bậc nhất có hệ số của biến bằng – 2 và hệ số tự do bằng 6;

b) Đa thức bậc hai có hệ số tự do bằng 4;

c) Đa thức bậc bốn có hệ số của lũy thừa bậc 3 của biến bằng 0;

d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0.

#Toán lớp 7

1

HQ

Hà Quang Minh

Giáo viên

17 tháng 9 2023

a) Đa thức bậc nhất có hệ số của biến bằng – 2 và hệ số tự do bằng 6 tức $a = - 2;b = 6$

$ - 2x + 6$.

b) Đa thức bậc hai có hệ số tự do bằng 4: ${x^2} + x + 4$.

c) Đa thức bậc bốn có hệ số của lũy thừa bậc 3 của biến bằng 0: ${x^4} + 0.{x^3} + {x^2} + 1 = {x^4} + {x^2} + 1$.

d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0: ${x^6} + 0.{x^5} + {x^4} + 0.{x^3} + {x^2} + 0.x = {x^6} + {x^4} + {x^2}$.

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP