cho hình chữ nhật abcd có e thuộc ad,f thuộc ab.Gọi i,k,m,n lần lượt là trung điểm của ef,fd,be,bd.Chứng minh: IN=KM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

30 tháng 3 2019
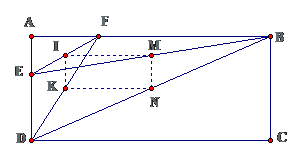
Ta đi chứng minh tứ giác IKMN là hình chữ nhật
+) Theo giả thiết có : là hình bình hành
+) là hình chữ nhật
Xét tam giác FEB ta có
\(\hept{\begin{cases}EI=IF\left(gt\right)\\EM=MB\left(gt\right)\end{cases}}\)
=> IM là đường trung bình của tam giác FEB
IM=1/2FB
\(\hept{\begin{cases}IMsongsongFB\\màAnằmtrenFB\end{cases}}\)
=> IM // AB(1)
Xét tam giác FDB có
\(\hept{\begin{cases}DK=KF\left(gt\right)\\DN=NB\left(gt\right)\end{cases}}\)
=>KN là đường trung bình cảu tam giác FDB
=> KN = 1/2 DB
\(\hept{\begin{cases}IM=\frac{1}{2}FB\left(cmt\right)\\KN=\frac{1}{2FB}\left(cmt\right)\end{cases}}\)
=>IM=KN(2)
Từ (1) và (2) => IMKN là hình bình hành
Xét tam giác EFD có
\(\hept{\begin{cases}EI=IF\left(gt\right)\\DK=KF\left(gt\right)\end{cases}}\)
=> IK là đường trung bình của tam giác EFD
\(\hept{\begin{cases}=>IKsongsongED\\màĂtrenED\end{cases}}\)
\(\hept{\begin{cases}=>IKsongsongDA\\ADvuonggocAB\left(hìnhchunhatABCD\right)\end{cases}}\)
\(\hept{\begin{cases}=>IKvuonggocAB\\IMsongsongAB\left(cmt\right)\end{cases}}\)
=>IM vuông góc IK
=> IKMN là hình chữ nhật
=>IN=KM