Giải phương trình nghiệm nguyên
y2+y=x4+x3+x2+x.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt x2−2x+m=tx2−2x+m=t, phương trình trở thành t2−2t+m=xt2−2t+m=x
Ta có hệ {x2−2x+m=tt2−2t+m=x{x2−2x+m=tt2−2t+m=x
⇒(x−t)(x+t−1)=0⇒(x−t)(x+t−1)=0
⇔[x=tx=1−t⇔[x=tx=1−t
⇔[x=x2−2x+mx=1−x2+2x−m⇔[x=x2−2x+mx=1−x2+2x−m
⇔[m=−x2+3xm=−x2+x+1⇔[m=−x2+3xm=−x2+x+1
Phương trình hoành độ giao điểm của y=−x2+x+1y=−x2+x+1 và y=−x2+3xy=−x2+3x:
−x2+x+1=−x2+3x−x2+x+1=−x2+3x
⇔x=12⇒y=54⇔x=12⇒y=54
Đồ thị hàm số y=−x2+3xy=−x2+3x và y=−x2+x+1y=−x2+x+1:

Ta thấy x = 1 không phải nghiệm của phương trình nên nhân 2 vế của phương trình với x - 1 ta có:
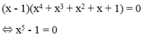
⇔ x = 1(KTM)
Vậy phương trình đã cho vô nghiệm.


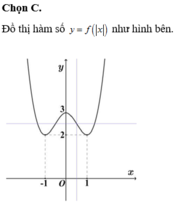
Đồ thị hàm số có điểm uốn là trung điểm của 2 đường cực trị I 1 2 ; 5 2
Số nghiệm của phương trình f(|x|)=m là số giao điểm của đồ thị hàm số y=f(|x|) và đường thẳng y=m. Để phương trình có 4 nghiệm thỏa mãn điều kiện đề bài thì 5 2 ≤ m < 3