Cho đoạn thẳng AB = 12cm. C là trung điểm của AB. Gọi I và K lần lượt là trung điểm của AC và BC. Tính độ dài đoạn thẳng IK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 12 2015
ta có C là trung điểm của A và B
suy ra AC=CB=AB/2
suy ra AC=CB= 12 cm/2
suy ra AC=CB =6cm
ta có I là trung điểm của A và B
suy ra IC=AC/2
suy ra IC=6cm/2
suy ra IC=3cm
lại có K là trung điểm của BC
suy ra CK=BC/2
suy ra CK=6cm/2
suy
ra CK=3cm
lại có BA và BC là 2 tia đối nhau
mà I thuộc BA ;K thuộc BC suy ra C nằm giữa
suy ra IC+CK=IK
thay IC=3cm;CK=3cm
suy ra IK=3cm+3cm
suy ra IK=6cm
NH
7 tháng 12 2019
hình tự vẽ
a, Trên cùng một nửa mặt phẳng bờ chứa tia Ax có AB < AC (4cm < 8cm)
=> B nằm giữa A, C (1)
=> AB + BC = AC
=> 4 + BC = 8
=> BC = 4 cm
b, Vì BC = AB = 4 cm
Và B nằm giữa A, C (2)
=> B là trung điểm của AC
c, Vì I là trung điểm của AB
=> I nằm giữa A , B (3)
=> IA = IB = AB/2
Vì K là trung điểm của BC
=> K nằm giữa B, C (4)
=> BK = KC = BC/2
Mà BC = AB
=> BC/2 = AB/2
=> IB = BK
Từ (1), (2), (3), (4) => B nằm giữa I, K
=> B là trung điểm của IK
CM
6 tháng 10 2017
Đáp án là C
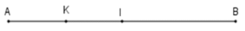
Vì điểm I là trung điểm đoạn thẳng AB nên AI = (1/2)AB = (1/2).8 = 4cm
Vì điểm K là trung điểm đoạn thẳng AI nên AK = IK = (1/2)AI = (1/2).4 = 2cm
Vậy: IK = 2cm
27 tháng 2 2022
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
b: BH=CH=BC/2=6cm
=>AH=8cm
c: Xét ΔAEH có
AK là đường cao
AK là đường trung tuyến
Do đó: ΔAEH cân tại A
hay AH=AE(1)
Xét ΔADH có
AI là đường cao
AI là đường trung tuyến
Do đó; ΔADH cân tại A
hay AD=AH(2)
Từ (1) và (2) suy ra AD=AE
hay ΔADE cân tại A
d: Xét ΔAHI vuông tại I và ΔAHK vuông tại K có
AH chung
\(\widehat{IAH}=\widehat{KAH}\)
Do đó: ΔAHI=ΔAHK
Suy ra: HI=HK
=>HD=HE
hay H nằm trên đường trung trực của DE(3)
Ta có: AD=AE
nên A nằm trên đường trung trực của DE(4)
Từ (3) và (4) suy ra AH là đường trung trực của DE