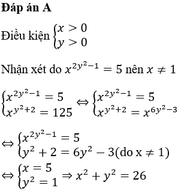Tìm x, y nguyên để x2+y2+x2y2-5xy+12=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2V
1
NV
2 tháng 3 2023
\(x^2y^2-x^2-3y^2-2x-1=0\)
\(\Leftrightarrow y^2\left(x^2-3\right)-\left(x+1\right)^2=0\)
\(\Leftrightarrow y^2\left(x^2-3\right)=\left(x+1\right)^2\left(1\right)\)
Vì y2 và (x+1)2 đều là các số chính phương, do đó x2-3 cũng phải là số chính phương.
Đặt \(x^2-3=a^2\) (a là số tự nhiên).
\(\Leftrightarrow\left(x-a\right)\left(x+a\right)=3\)
Ta có x+a>x-a. Lập bảng:
| x+a | 3 | -1 |
| x-a | 1 | -3 |
| x | 2 | -2 |
Với \(x=2\) . \(\left(1\right)\Rightarrow y^2=9\Leftrightarrow y=\pm3\)
Với \(x=-2\). \(\left(1\right)\Rightarrow y^2=1\Leftrightarrow y=\pm1\)
Vậy các số nguyên \(\left(x;y\right)=\left(2;3\right),\left(2;-3\right),\left(-2;1\right),\left(-2;-1\right)\)
11 tháng 7 2020
Trả lời:
Phương trình hoành độ giao điểm (P) và (d) ta có:
\(-x^2=2x+m-1\)
\(\Leftrightarrow x^2+2x+m-1=0\)(1)
Ta có: \(\Delta=2^2-4.1.\left(m-1\right)\)
\(=4-4m+4\)
\(=8-4m\)
Để phương trình (1) có 2 nghiệm phân biệt \(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow8-4m>0\)
\(\Leftrightarrow4m< 8\)
\(\Leftrightarrow m< 2\)
\(\Rightarrow\)Phương trình (1) có 2 nghiệm phân biệt
\(\Rightarrow\)(d) cắt (P) tại 2 diểm phân biệt \(A\left(x_1,y_1\right);B\left(x_2,y_2\right)\)
Áp dụng Vi-ét \(\hept{\begin{cases}x_1+x_2=-2\left(1\right)\\x_1.x_2=m-1\left(2\right)\end{cases}}\)
Ta có \(y_1=-x_1^2\); \(y_2=-x_2^2\)
Theo đề bài:
\(x_1.y_1-x_2.y_2-x_1.x_2=4\)
\(\Leftrightarrow x_1.\left(-x_1^2\right)-x_2.\left(-x_2^2\right)-x_1.x_2=4\)
\(\Leftrightarrow-x_1^3+x_2^3-x_1.x_2=4\)
\(\Leftrightarrow-\left(x_1^3-x_2^3\right)-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left(x_1^2+x_1.x_2+x_2^2\right)-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right)\left[\left(x_1+x_2\right)^2-2x_1.x_2+x_1.x_2\right]-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left[\left(x_1+x_2\right)^2-x_1.x_2\right]-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left[\left(-2\right)^2-m+1\right]-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left(4-m+1\right)=4+m-1\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left(3-m\right)=m+3\)
\(\Leftrightarrow-\left(x_1-x_2\right)=\frac{m+3}{3-m}\)
\(\Leftrightarrow x_1-x_2=\frac{m+3}{m-3}\)(3)
Từ (1) (3) ta có: \(\hept{\begin{cases}x_1+x_2=-2\\x_1-x_2=\frac{m+3}{m-3}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x_1=-2+\frac{m+3}{m-3}=\frac{9-m}{m-3}=-\left(m+3\right)\\x_1+x_2=-2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1=\frac{-\left(m+3\right)}{2}\\x_2=\frac{m-1}{2}\end{cases}}\)
Thay x1, x2 vào (2) ta có
\(x_1.x_2=m-1\)
\(\Leftrightarrow\frac{-\left(m+3\right)}{2}.\frac{m-1}{2}=m-1\)
\(\Leftrightarrow\frac{-\left(m+3\right)}{2}=2\)
\(\Leftrightarrow-\left(m+3\right)=4\)
\(\Leftrightarrow m+3=-4\)
\(\Leftrightarrow m=-7\)(TM)
Vậy \(m=-7\) thì thỏa mãn bài toán
23 tháng 3 2017
2,
M + N = 3xyz - 3x2 + 5xy - 1 + 5x2 + xyz - 5xy + 3 - y
= -3x2 + 5x2 + 3xyz + xyz + 5xy - 5xy - y - 1 + 3
= 2x2 + 4xyz - y +2.
M - N = (3xyz - 3x2 + 5xy - 1) - (5x2 + xyz - 5xy + 3 - y)
= 3xyz - 3x2 + 5xy - 1 - 5x2 - xyz + 5xy - 3 + y
= -3x2 - 5x2 + 3xyz - xyz + 5xy + 5xy + y - 1 - 3
= -8x2 + 2xyz + 10xy + y - 4.
N - M = (5x2 + xyz - 5xy + 3 - y) - (3xyz - 3x2 + 5xy - 1)
= 5x2 + xyz - 5xy + 3 - y - 3xyz + 3x2 - 5xy + 1
= 5x2 + 3x2 + xyz - 3xyz - 5xy - 5xy - y + 3 + 1
= 8x2 - 2xyz - 10xy - y + 4.
3,
a) P + (x2 – 2y2) = x2 – y2 + 3y2 – 1
P = (x2 – y2 + 3y2 – 1) - (x2 – 2y2)
P = x2 – y2 + 3y2 – 1 - x2 + 2y2
P = x2 – x2 – y2 + 3y2 + 2y2 – 1
P = 4y2 – 1.
Vậy P = 4y2 – 1.
b) Q – (5x2 – xyz) = xy + 2x2 – 3xyz + 5
Q = (xy + 2x2 – 3xyz + 5) + (5x2 – xyz)
Q = xy + 2x2 – 3xyz + 5 + 5x2 – xyz
Q = 7x2 – 4xyz + xy + 5
Vậy Q = 7x2 – 4xyz + xy + 5.
4,
a, Thu gọn : x2+2xy-3x3+2y3+3x3-y3
= x2+2xy+(-3x3+3x3)+2y3-y3
=x2+2xy+2y3-y3
Thay x=5,y=4 vào đa thức x2+2xy+2y3-y3 Ta có:
52 + 2.5.4 + 43 = 25 + 40 + 64 = 129.
Vậy giá trị của đa thức x2+2xy+2y3-y3 tại x=5,y=4 là 129
b,
Thay x = -1; y = -1 vào biểu thức xy-x2y2+x4y4-x6y6+x8y8 Ta Có
M = (-1)(-1) - (-1)2.(-1)2 + (-1)4. (-1)4-(-1)6.(-1)6 + (-1)8.(-1)8
= 1 -1 + 1 - 1+ 1 = 1.
Vậy giá trị của biểu thức xy-x2y2+x4y4-x6y6+x8y8 tại x=-1, y=-1 là 1
5,
a, C=A+B
C = x2 – 2y + xy + 1 + x2 + y - x2y2 - 1
C = 2x2 – y + xy - x2y2
b) C + A = B => C = B - A
C = (x2 + y - x2y2 - 1) - (x2 – 2y + xy + 1)
C = x2 + y - x2y2 - 1 - x2 + 2y - xy - 1
C = - x2y2 - xy + 3y - 2.
NN
1
12 tháng 6 2023
Với x, y là hai số dương, dễ dàng chứng minh x + y 2,
do x + y = 2 => 0 < xy ≤ 1 (1)
Ta lại có: 2xy( x2 + y2) ≤
=> 0 < 2xy(x2 + y2) ≤ (x+y)4/4 = 4
=> 0 < xy( x2 + y2) ≤ 2 (2)
Nhân (1) với (2) theo vế ta có: x2y2 ( x2 + y2) ≤ 2 (đpcm)
Dấu “=” xảy ra khi x = y = 1
TV
1
16 tháng 1 2021
Nếu x, y không chia hết cho 3 thì x2 chia cho 3 dư 1, do đó \(\left(x^2+2\right)^2\) chia hết cho 3.
Mà \(2y^4+11y^2+x^2y^2+9\) không chia hết cho 3 nên suy ra vô lí.
Do đó x = 3 hoặc y = 3 (Do x, y là các số nguyên tố).
Với x = 3 ta có \(2y^4+20y^2+9=121\Leftrightarrow y^4+10y^2-56=0\Leftrightarrow\left(y^2-4\right)\left(y^2+14\right)=0\Leftrightarrow y=2\) (Do y là số nguyên tố).
Với y = 3 ta có:
\(\left(x^2+2\right)^2=9x^2+270\Leftrightarrow x^4-5x^2-266=0\Leftrightarrow\left(x^2+14\right)\left(x^2-19\right)=0\). Không tồn tại số nguyên tố x thoả mãn.
Vậy x = 2; y = 3.
3 tháng 6 2017
- xét phương trình hoành độ giao điểm : \(x^2=\left(2m-1\right)x-m+2\)\(\Leftrightarrow x^2-\left(2m-1\right)x+m-2=0\)có \(\Delta=\left(2m-1\right)^2-4\left(m-2\right)=4m^2-8m+9=\left(2m-1\right)^2+8\ge8\)vậy nên phương trinh luôn có 2 nghiệm phân biệt tức hai đồ thị luôn cắt nhau tại 2 điểm phân biệt A và B
- Có viet : \(\hept{\begin{cases}x_1+x_2=2m-1\\x_1x_2=m-2\end{cases}}\)ta có : \(A\left(x_1,y_1\right)=A\left(x_1,x_1^2\right)\)và \(B\left(x_2,y_2\right)=B\left(x_2,x_2^2\right)\)
nên ta có : \(x_1y_1+x_2y_2=0\Leftrightarrow x_1^3+x_2^3=0\)\(\Leftrightarrow\left(x_1+x_2\right)\left(\left(x_1+x_2\right)^2-3x_1x_2\right)=0\)\(\Leftrightarrow\left(2m-1\right)\left[\left(2m-1\right)^2-3m+6\right]=0\)
- \(2m-1=0\Leftrightarrow m=\frac{1}{2}\)
- \(\left(2m-1\right)^2-3m+6=0\Leftrightarrow4m^2-7m-7=0\)VN
28 tháng 2 2019
2. Cho parabol (P): y = x2 và đường thẳng (d): y = 2(m – 1)x + m2 + 2m (m là tham số, m ∈ R )
a) Chứng minh rằng đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt A, B?
b) Gọi H và K lần lượt là hình chiếu của A và B trên trục hoành.
Tìm m sao cho: OH2 + OK2 = 6 mọi người hướng dẫ mk ý b vs