Tìm k để pt (k+2)x2 - 2kx-k = 0 có 2 nghiệm mà sắp xếp trên trục số chúng đối xứng nhau qua điểm x = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\text{Δ}=\left(2k\right)^2-4\cdot\left(k^2-k\right)\)
\(=4k^2-4k^2+4k\)
=4k
Để phương trình có nghiệm thì \(4k\ge0\)
hay \(k\ge0\)

Thay \(x=2-\sqrt{3}\) vào Pt, ta được:
\(\left(2-\sqrt{3}\right)^2-3\left(2-\sqrt{3}\right)+k-1=0\)
\(\Leftrightarrow7-4\sqrt{3}-6+3\sqrt{3}+k-1=0\)
\(\Leftrightarrow k-\sqrt{3}=0\)
hay \(k=\sqrt{3}\)
\(x_1+x_2=3\)
nên \(x_2=3-2+\sqrt{3}=\sqrt{3}+1\)

a,thay k=0 vào PT ta có
\(9x^2-25=0\)
\(\Leftrightarrow9\left(x^2-\left(\frac{5}{3}\right)^2\right)=0\)
\(\Leftrightarrow9\left(x-\frac{5}{3}\right)\left(x+\frac{5}{3}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-\frac{5}{3}=0\\x+\frac{5}{3}=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{5}{3}\\x=-\frac{5}{3}\end{cases}}\)
b,thay x=1 vào PT ta có
\(9-25-k^2-2k=0\)
\(\Leftrightarrow k^2+2k+16=0\)
\(\Leftrightarrow\left(k+1\right)^2+15\ge0\)
Vậy ko có giá tri k thỏa mãn ĐK bài toán
`Answer:`
`a)` Thay `k=0` vào phương trình được:
`9x^2-25=0`
`<=>(3x-5)(3x+5)=0`
`<=>3x+5=0` hoặc `3x-5=0`
`<=>x=-5/3` hoặc `x=5/3`
`b)` Thay `x=-1` vào phương trình được:
`9-25-k^2+2k=0`
`<=>-k^2+2k-16=0`
`<=>-(k^2-2k+1)-15=0`
`<=>-(k-1)^2-15=0`
Mà `-(k-1)^2<=0∀k=>-(k-1)^2-15<0`
Vậy phương trình vô nghiệm.

mình làm luôn 4 nghiệm nhé-đổi k thành m cho dễ nhé
Pt trở thành: t² + 2mt + 4 = 0 (*).
Pt đã cho có 4 nghiệm phân biệt <=> pt (*) có 2 nghiệm phân biệt dương. => xảy ra đồng thời: delta’(t) > 0; S = x1 + x2 > 0; p = x1x2 > 0 <=> m² - 4 > 0; -2m > 0; 4 > 0 ( theo Vi-et)
=> m < -2.
=> pt đã cho có nghiệm x1,2 = +- căn t1; x3,4 = +- căn t2
=> x1^4 = x2^4 = t1²; x3^4 = x4^4 = t2²
=> x1^4 + x2^4 + x3^4 + x4^4 = 2(t1² + t2²) = 32 => t1² + t2² = 16.
<=> (t1 + t2)² - 2t1t2 = 16 <=> (-2m)² - 2.4 = 16 <=> 4m² - 4 = 16
<=> m² = 6, mà m < -2 => m = -(căn 6).
vậy với m = -(căn 6) thì pt đã cho có 4 nghiệm phân biệt x1 ,x2, x3, x4 thỏa mãn x1^4 + x2^4 + x3^4 + x4^4 = 32.
mik lm 4 nghiệm nhé-đổi k thành m nữa
Pt trở thành: t² + 2mt + 4 = 0 (*).
Pt đã cho có 4 nghiệm phân biệt <=> pt (*) có 2 nghiệm phân biệt dương. => xảy ra đồng thời: delta’(t) > 0; S = x1 + x2 > 0; p = x1x2 > 0 <=> m² - 4 > 0; -2m > 0; 4 > 0 ( theo Vi-et)
=> m < -2.
=> pt đã cho có nghiệm x1,2 = +- căn t1; x3,4 = +- căn t2
=> x1^4 = x2^4 = t1²; x3^4 = x4^4 = t2²
=> x1^4 + x2^4 + x3^4 + x4^4 = 2(t1² + t2²) = 32 => t1² + t2² = 16.
<=> (t1 + t2)² - 2t1t2 = 16 <=> (-2m)² - 2.4 = 16 <=> 4m² - 4 = 16
<=> m² = 6, mà m < -2 => m = -(căn 6).
vậy với m = -(căn 6) thì pt đã cho có 4 nghiệm phân biệt x1 ,x2, x3, x4 thỏa mãn x1^4 + x2^4 + x3^4 + x4^4 = 32.

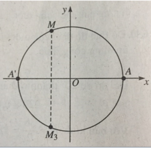
-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B

a: Vì a=-1<0 nên hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (-∞;2]
Bảng biến thiên là:
| x | -∞ | 2 | +∞ |
| y | -∞ | 1 | -∞ |



\(\left\{{}\begin{matrix}k\ne-2\\\Delta'=k^2+k\left(k+2\right)>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k\ne-2\\\left[{}\begin{matrix}k\ge0\\k\le-1\end{matrix}\right.\end{matrix}\right.\)
Theo định lý Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=\frac{2k}{k+2}\\x_1x_2=\frac{-k}{k+2}\end{matrix}\right.\)
\(\frac{x_1+x_2}{2}=1\)
\(\Leftrightarrow x_1+x_2=2\)
\(\Leftrightarrow\frac{2k}{k+2}=2\)
\(\Leftrightarrow2k=2k+4\)
Không tồn tại k thỏa mãn