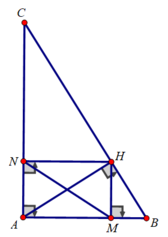
Tam giác ABC vuông tại A , đường cao AH, vẽ HM vuông góc với AB , HN vuông góc với AC , biết AB=3cm, AC=4cm a) tính độ dài MN b) tính số đo các góc tam giác AMN c) tính diện tích BMNC giúp mik với🙇♀️
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 7 2019
b) Xét tam giác AHB vuông tại H, HM là đường cao có:
∠(AMN) + ∠(ANM ) = 90 0 ⇒ ∠(ANM ) = 90 0 - ∠(AMN) = 53 , 1 0
21 tháng 7 2023
a: BC=căn 6^2+8^2=10cm
AH=6*8/10=4,8cm
c:
Xét tứ giác ANHM có
góc ANH=góc AMH=góc MAN=90 độ
=>ANHM là hình chữ nhật
AD vuông góc MN
=>góc DAC+góc ANM=90 độ
=>góc DAC+góc AHM=90 độ
=>góc DAC+góc ABC=90 độ
=>góc DAC=góc DCA
=>DA=DC
góc DAC+góc DAB=90 độ
góc DCA+góc DBA=90 độ
mà góc DAC=góc DCA
nên góc DAB=góc DBA
=>DA=DB
=>DB=DC
=>D là trung điểm của BC
19 tháng 10 2021
c: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
10 tháng 3 2022
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: BC=10cm
AH=4,8cm
c: Xét ΔABH vuông tại H có HM là đườg cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔACH vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
hay AM/AC=AN/AB
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
AM/AC=AN/AB
Do đó: ΔAMN\(\sim\)ΔACB
10 tháng 3 2022
\(a)\) Xét \(\Delta ABC\) và \(\Delta HBA:\)
\(\widehat{BAC}=\widehat{BHA}\left(=90^o\right).\\ \widehat{ABC}chung.\\ \Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right).\)
\(b)\) Xét \(\Delta ABC\) vuông tại A:
\(+)BC^2=AB^2+AC^2\left(Pytago\right).\\ \Rightarrow BC^2=6^2+8^2=36+64=100.\\ \Rightarrow BC=10\left(cm\right).\)\(+)AH.BC=AB.AC\) (Hệ thức lượng).\(\Rightarrow AH.10=6.8.\\ \Rightarrow AH=4,8\left(cm\right).\)\(c)\) Xét \(\Delta ABH\) vuông tại H, đường cao MH:\(AH^2=AM.AB\) (Hệ thức lượng). \(\left(1\right)\)Xét \(\Delta ACH\) vuông tại H, đường cao NH:\(AH^2=AN.AC\) (Hệ thức lượng). \(\left(2\right)\)Từ \(\left(1\right);\left(2\right)\Rightarrow AM.AB=AN.AC.\)Xét \(\Delta ACB\) và \(\Delta AMN:\)\(\Rightarrow\dfrac{AB}{AN}=\dfrac{AC}{AM}.\)\(\widehat{A}chung.\\ \dfrac{AB}{AN}=\dfrac{AC}{AM}\left(cmt\right).\\ \Rightarrow\Delta ACB\sim\Delta AMN\left(c-g-c\right).\)
16 tháng 12 2023
a: Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\left(1\right)\)
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>\(BC=\sqrt{625}=25\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot25=15\cdot20=300\)
=>\(AH=\dfrac{300}{25}=12\left(cm\right)\)
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(3\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(4\right)\)
Từ (3) và (4) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN đồng dạng với ΔACB
c: Ta có: ΔABC vuông tại A
mà AK là đường trung tuyến
nên AK=KC=KB
Ta có: KA=KC
=>ΔKAC cân tại K
=>\(\widehat{KAC}=\widehat{KCA}\)
Ta có: ΔAMN đồng dạng với ΔACB
=>\(\widehat{ANM}=\widehat{ABC}\)
Ta có: \(\widehat{KAC}+\widehat{ANM}\)
\(=\widehat{ABC}+\widehat{KCA}=90^0\)
=>AK\(\perp\)MN tại I
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2;CH\cdot BC=CA^2\)
=>\(BH\cdot25=15^2=225;CH\cdot25=20^2=400\)
=>BH=225/25=9(cm); CH=400/25=16(cm)
Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\)
=>\(AM\cdot15=12^2\)=144
=>AM=144/15=9,6(cm)
Ta có: AMHN là hình chữ nhật
=>AH=MN
mà AH=12cm
nênMN=12cm
Ta có: ΔANM vuông tại A
=>\(AN^2+AM^2=NM^2\)
=>\(AN^2+9,6^2=12^2\)
=>AN=7,2(cm)
Xét ΔIMA vuông tại I và ΔAMN vuông tại A có
\(\widehat{IMA}\) chung
Do đó: ΔIMA đồng dạng với ΔAMN
=>\(\dfrac{S_{IMA}}{S_{AMN}}=\left(\dfrac{AM}{MN}\right)^2=\left(\dfrac{4}{5}\right)^2=\dfrac{16}{25}\)
=>\(S_{IMA}=\dfrac{16}{25}\cdot\dfrac{1}{2}\cdot AM\cdot AN=22,1184\left(cm^2\right)\)
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
hay AH=2,4(cm)
Xét tứ giác AMHN có
\(\widehat{MAN}=\widehat{ANH}=\widehat{AMH}=90^0\)
Do đó: AMHN là hình chữ nhật
Suy ra: AH=MN=2,4(cm)