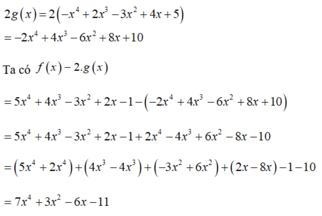Tìm GTNN của biểu thức M=x4-2x3+3x2-4x-5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
17 tháng 10 2023
Sửa đề:
\(E=x^4-2x^3+3x^2-4x+2022\)
\(=\left(x^4-2x^3+x^2\right)+\left(2x^2-4x+2\right)+2020\)
\(=\left(x^2-x\right)^2+2\left(x-1\right)^2+2020\)
Vì \(\left(x^2-x\right)^2+2\left(x-1\right)^2\ge0\forall x\)
\(\Rightarrow E\ge2020\)
\(MinE=2020\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\end{matrix}\right.\)\(\Leftrightarrow x=1\)
CM
15 tháng 3 2017
Ta có p(x) + q(x)
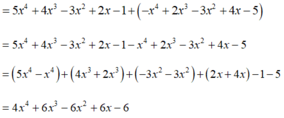
Bậc của đa thức p ( x ) + q ( x ) = 4 x 4 + 6 x 3 - 6 x 2 + 6 x - 6 l à 4
Chọn đáp án C
CM
7 tháng 5 2019
+) Ta có
2 g ( x ) = 2 − x 4 + 2 x 3 − 3 x 2 + 4 x + 5 = − 2 x 4 + 4 x 3 − 6 x 2 + 8 x + 10 Ta có f ( x ) − 2 ⋅ g ( x ) = 5 x 4 + 4 x 3 − 3 x 2 + 2 x − 1 − − 2 x 4 + 4 x 3 − 6 x 2 + 8 x + 10 = 5 x 4 + 4 x 3 − 3 x 2 + 2 x − 1 + 2 x 4 − 4 x 3 + 6 x 2 − 8 x − 10 = 5 x 4 + 2 x 4 + 4 x 3 − 4 x 3 + − 3 x 2 + 6 x 2 + ( 2 x − 8 x ) − 1 − 1 = 7 x 4 + 3 x 2 − 6 x − 11
Hệ số cần tìm là -11
Chọn đáp án C
TH
3
MH
17 tháng 10 2023
Câu E bạn xem lại đề nha
F=\(-y^2+2y-6\)
\(=-\left(y^2-2y+6\right)\)
\(=-\left(y-1\right)^2-5\)
Vì \(-\left(y-1\right)^2\le0\forall y\)
\(\Rightarrow F\le-5\forall y\)
\(MaxF=-5\Leftrightarrow y=1\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
17 tháng 10 2023
\(F=-y^2+2y-6=-\left(y^2-2y+1\right)-5=-\left(y-1\right)^2-5\le-5\forall y\in R\\ Vậy:max_F=-5\Leftrightarrow y=1\)
CM
30 tháng 12 2017
Thu gọn Q(x) = 5x4 - x5 - x2 - 2x3 + 3x2 + 3x - 2x4 + 5
= -x5 + 3x4 - 2x3 + 2x2 + 3x + 5
Hệ số của x4là 3. Chọn B
H
21 tháng 3 2023
`a,A(x) =2x^3 -x^4 +2x-4+3x^2 -2x^3+x^4`
`= ( 2x^3-2x^3) +(-x^4+x^4) + 2x -4+3x^2`
`= 0+0+ 2x -4+3x^2`
`= 3x^2 +2x-4`
`b, M(x)=A(x)+B(x)`
`M(x)= 3x^2 +2x-4 + x-2`
`= 3x^2 + 3x-6`
`b, N(x) = A(x) - B(x)`
`N(x)= 3x^2 +2x-4 -(x-2)`
`= 3x^2 +2x-4 -x+2`
`= 3x^2 + x -2`
`c,` Ta có :
`x-2=0`
`=> x=0+2`
`=>x=2`