Tính giá trị nhỏ nhất: B=3x2 -11x +15
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 10 2017
B = 9 x - 3 x 2 = 3 3 x - x 2 = 3 9 / 4 - 9 / 4 + 2 . 3 / 2 x - x 2
= 3 9 / 4 - 9 / 4 - 3 / 2 x + x 2
= 3 9 / 4 - 3 / 2 x - x 2 = 27 / 4 - 3 / 2 - x 2
Vì 3 / 2 - x 2 ≥ 0 với mọi x
⇒ B = 27/4 − 3 / 2 - x 2 ≤ 27/4 do đó giá trị lớn nhất của B bằng 27/4 tại x = 3/2
CM
1 tháng 5 2019
Chọn A
Xét hàm số y = x 3 - 3 x 2 trên đoạn [-2;1].
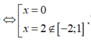
Ta có: 
Do hàm số đã cho liên tục trên [-2;1] nên 
Vậy T = M + m = -20.
CM
18 tháng 1 2017
Đáp án A
Ta có: y ' = 3 x 2 − 6 x = 0 ⇔ x = 0 x = 2 l o a i . Hàm số đã cho liên tục và xác định trên − 2 ; 1
Lại có y − 2 = − 20 ; y 0 = 0 ; y 1 = − 2. Do đó T = 0 − 20 = − 20
CM
8 tháng 5 2019
Theo bài toán ta có thể suy ra BBT của đồ thị hàm số y = f (x) như sau:
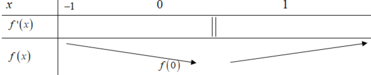
Dễ thấy trong các đáp án A, C, D đều sai. Hàm số đạt cực tiểu tại x = 0.
Chọn B
QH
0
CM
1 tháng 7 2017
Đáp án B
Phương pháp:
- Tìm TXĐ
- Tìm nghiệm và các điểm không xác định của y’.
- Tính giá trị của hàm số tại các điểm trên, từ đó đánh giá giá trị nhỏ nhất của hàm số trên đoạn [1;3]
Cách giải:
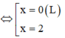
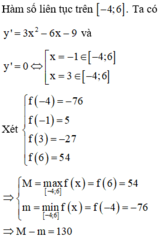
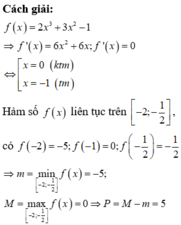
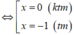
\(B=3\left(x^2-\frac{11}{3}x+5\right)\)
\(=3\left(x^2-\frac{11}{3}x+\frac{121}{36}+\frac{59}{36}\right)=3\left(x-\frac{11}{6}\right)^2+\frac{59}{12}\)
\(\ge\frac{59}{12}\)