Cho A = 4x - x2. Tính giá trị lớn nhất của A.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B.
Phương pháp:
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
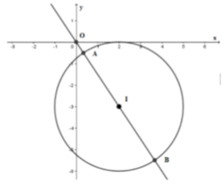
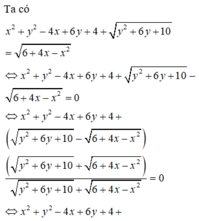
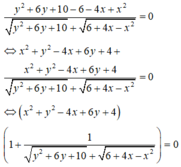


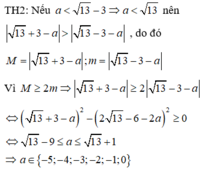


A=-(x^2-4x+4-4)
=-(x-2)^2+4<=4
Dấu = xảy ra khi x=2
B=-(x^2-4x-2)
=-(x^2-4x+4-6)
=-(x-2)^2+6<=6
Dấu = xảy ra khi x=2

`#3107.101107`
`A = -x^2 + 4x - 8`
`= -(x^2 - 4x + 8)`
`= - [ (x^2 - 2*x*2 + 2^2) + 4]`
`= - [ (x - 2)^2 + 4]`
`= -(x-2)^2 - 4`
Vì `-(x - 2)^2 \le 0` `AA` `x`
`=> -(x - 2)^2 - 4 \ge 0` `AA` `x`
Vậy, GTLN của A là `-4` khi `(x - 2)^2 = 0`
`<=> x - 2 = 0`
`<=> x = 2.`
A = -x² + 4x - 8
= -(x² - 4x + 8)
= -(x² - 4x + 4 + 4)
= -[(x - 2)² + 4]
= -(x - 2)² - 4
Do (x - 2)² ≥ 0 với mọi x R
⇒ -(x - 2)² ≤ 0 với mọi x ∈ R
⇒ -(x - 2)² - 4 ≤ -4 với mọi x ∈ R
Vậy GTLN của A là -4 khi x = 2

Chọn C
Hàm số y =
x
2
+
x
+
4
x
+
1
là hàm phân thức có tập xác định là ![]() nên nó liên tục trên [0;2], từ đó ta vận dụng quy tắc tìm giá trị lớn nhất và nhỏ nhất không cần xét dấu đạo hàm.
nên nó liên tục trên [0;2], từ đó ta vận dụng quy tắc tìm giá trị lớn nhất và nhỏ nhất không cần xét dấu đạo hàm.
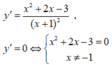
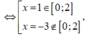
Ta có ![]()
=> A = 4, a = 3.
Vậy a + A = 7.

`A=x^2-4x+1`
`=x^2-4x+4-3`
`=(x-2)^2-3>=-3`
Dấu "=" xảy ra khi x=2
`B=4x^2+4x+11`
`=4x^2+4x+1+10`
`=(2x+1)^2+10>=10`
Dấu "=" xảy ra khi `x=-1/2`
`C=(x-1)(x+3)(x+2)(x+6)`
`=[(x-1)(x+6)][(x+3)(x+2)]`
`=(x^2+5x-6)(x^2+5x+6)`
`=(x^2+5x)^2-36>=-36`
Dấu "=" xảy ra khi `x=0\or\x=-5`
`D=5-8x-x^2`
`=21-16-8x-x^2`
`=21-(x^2+8x+16)`
`=21-(x+4)^2<=21`
Dấu "=" xảy ra khi `x=-4`
`E=4x-x^2+1`
`=5-4+4-x^2`
`=5-(x^2-4x+4)`
`=5-(x-2)^2<=5`
Dấu "=" xảy ra khi `x=5`

Tính giá trị nhỏ nhất:
\(A=x^2-4x+1=(x^2-4x+4)-3=(x-2)^2-3\)
Vì $(x-2)^2\geq 0, \forall x\in\mathbb{R}$ nên $A=(x-2)^2-3\geq 0-3=-3$
Vậy $A_{\min}=-3$
Giá trị này đạt tại $(x-2)^2=0\Leftrightarrow x=2$
$B=4x^2+4x+11=(4x^2+4x+1)+10=(2x+1)^2+10\geq 0+10=10$
Vậy $B_{\min}=10$
Giá trị này đạt tại $(2x+1)^2=0\Leftrightarrow x=-\frac{1}{2}$
$C=(x-1)(x+3)(x+2)(x+6)$
$=(x-1)(x+6)(x+3)(x+2)$
$=(x^2+5x-6)(x^2+5x+6)$
$=(x^2+5x)^2-36\geq 0-36=-36$
Vậy $C_{\min}=-36$. Giá trị này đạt $x^2+5x=0\Leftrightarrow x=0$ hoặc $x=-5$
Tìm giá trị lớn nhất:
$D=5-8x-x^2=21-(x^2+8x+16)=21-(x+4)^2$
Vì $(x+4)^2\geq 0, \forall x\in\mathbb{R}$ nên $D=21-(x+4)^2\leq 21$
Vậy $D_{\max}=21$. Giá trị này đạt tại $(x+4)^2=0\Leftrightarrow x=-4$
$E=4x-x^2+1=5-(x^2-4x+4)=5-(x-2)^2\leq 5$
Vậy $E_{\max}=5$. Giá trị này đạt tại $(x-2)^2=0\Leftrightarrow x=2$
\(A=4x-x^2=-\left(x^2-4x+4\right)+4\)
\(=-\left(x-2\right)^2+4\le4\)
\(maxA=4\Leftrightarrow x=2\)