53xy chia hết cho 5,9 nhưng ko chia hết cho 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
8 tháng 11 2021
a/
\(\overline{4x6y}⋮2;\overline{4x6y}⋮5\Rightarrow y=0\Rightarrow\overline{4x6y}=\overline{4x60}\)
\(\Rightarrow\overline{4x60}-1=\overline{4x59}⋮3\Rightarrow4+x+5+9=18+x⋮9\Rightarrow x=\left\{0;9\right\}\)
b/
\(\overline{57x2y}\) không chia hết cho 2 => y lẻ
\(\overline{57x2y}⋮5\Rightarrow y=5\)
\(\Rightarrow\overline{57x2y}=\overline{57x25}⋮9\Rightarrow5+7+x+2+5=19+x⋮9\Rightarrow x=8\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
16 tháng 10 2023
1) 17x2y chia hết cho 2,5,3 => y=0 (chia hết cho cả 2 và 5)
Ta có: 1+7+2=10 (chia 3 dư 1) => Để chia hết cho 3 thì x chia 3 dư 2
Vậy: x=2 hoặc x=5 hoặc x=8
Vậy: \(\left(x;y\right)=\left\{\left(2;0\right);\left(5;0\right);\left(8;0\right)\right\}\)
3, 234xy chia hết cho 2,5,9=> y=0
Ta có: 2+3+4=9 (chia hết cho 9) => Để chia hết cho 9 thì x chia hết cho 9
=> x=0 hoặc x=9
Vậy: \(\left(x;y\right)=\left\{\left(0;0\right);\left(9;0\right)\right\}\)
3, 4x6y chia hết cho 2,5 => y=0 (chia hết cho 2 và 5)
Vì: x-y=4 => x=4
Vậy: \(\left(x;y\right)=\left(4;0\right)\)
4, 57x2y chia hết cho 5,9 nhưng không chia hết cho 2
Vậy y chia hết cho 5 không chia hết cho 2 => y=5
Ta có: 5+7+2+5= 19 (chia 9 dư 1). Để số đó chia hết cho 9 thì x chia 9 dư 8 => x=8
Vậy: \(\left(x;y\right)=\left(8;5\right)\)
KV
16 tháng 10 2023
1) Để 17x2y chia hết cho cả 2 và 5 thì y = 0
Để 17x20 chia hết cho 3 thì 1 + 7 + x + 2 + 0 = 10 + x chia hết cho 3
⇒ x ∈ {2; 5; 8}
Vậy ta được các cặp giá trị (x; y) thỏa mãn là:
(2; 0); (5; 0); (8; 0)
2) Để 234xy chia hết cho 2 và 5 thì y = 0
Để 234x0 chia hết cho 9 thì 2 + 3 + 4 + x + 0 = 9 + x chia hết cho 9
⇒ x ∈ {0; 9}
Vậy ta được các cặp giá trị (x; y) thỏa mãn là:
(0; 0); (9; 0)
3) Để 4x6y chia hết cho 2 và 5 thì y = 0
Mà x - y = 4
⇒ x = 4
Vậy ta được cặp giá trị (x; y) thỏa mãn là (4; 0)
4) Để 57x2y chia hết cho 5 mà không chia hết cho 2 nên y = 5
Để 57x25 chia hết cho 9 thì 5 + 7 + x + 2 + 5 = 19 + x chia hết cho 9 thì x = 8
Vậy ta được cặp giá trị (x; y) thỏa mãn là:
(8; 5)
8 tháng 8 2023
Ví dụ: a = 6, b = 3. Ta có a chia hết cho 3 và b chia hết cho 3, nhưng (a+b) = 9 không chia hết cho 6.
Ví dụ: a = 9, b = 3. Ta có a chia hết cho 3 và b chia hết cho 3, nhưng (a+b) = 12 không chia hết cho 9.
Ví dụ: a = 2, b = 4. Ta có a chia hết cho 2 và b chia hết cho 4, nhưng (a+b) = 6 không chia hết cho 4.
Ví dụ: a = 2, b = 4. Ta có a chia hết cho 2 và b chia hết cho 4, nhưng (a+b) = 6 không chia hết cho 6.
Ví dụ: a = 6, b = 9. Ta có a chia hết cho 6 và b chia hết cho 9, nhưng (a+b) = 15 không chia hết cho 6.
Ví dụ: a = 6, b = 9. Ta có a chia hết cho 6 và b chia hết cho 9, nhưng (a+b) = 15 không chia hết cho 9.
Ví dụ: a = 2, b = 2. Ta có a chia hết cho 2 và b chia hết cho 2, nhưng (a+b) = 4 không chia hết cho 4.
😎 Ví dụ: a = 2, b = 2. Ta có a chia hết cho 2 và b chia hết cho 2, nhưng (a+b) = 4 không chia hết cho 6.
Ví dụ: a = 3, b = 9. Ta có a chia hết cho 3 và b chia hết cho 9, nhưng (a+b) = 12 không chia hết cho 9.
Ví dụ: a = 3, b = 9. Ta có a chia hết cho 3 và b chia hết cho 9, nhưng (a+b) = 12 không chia hết cho 6.
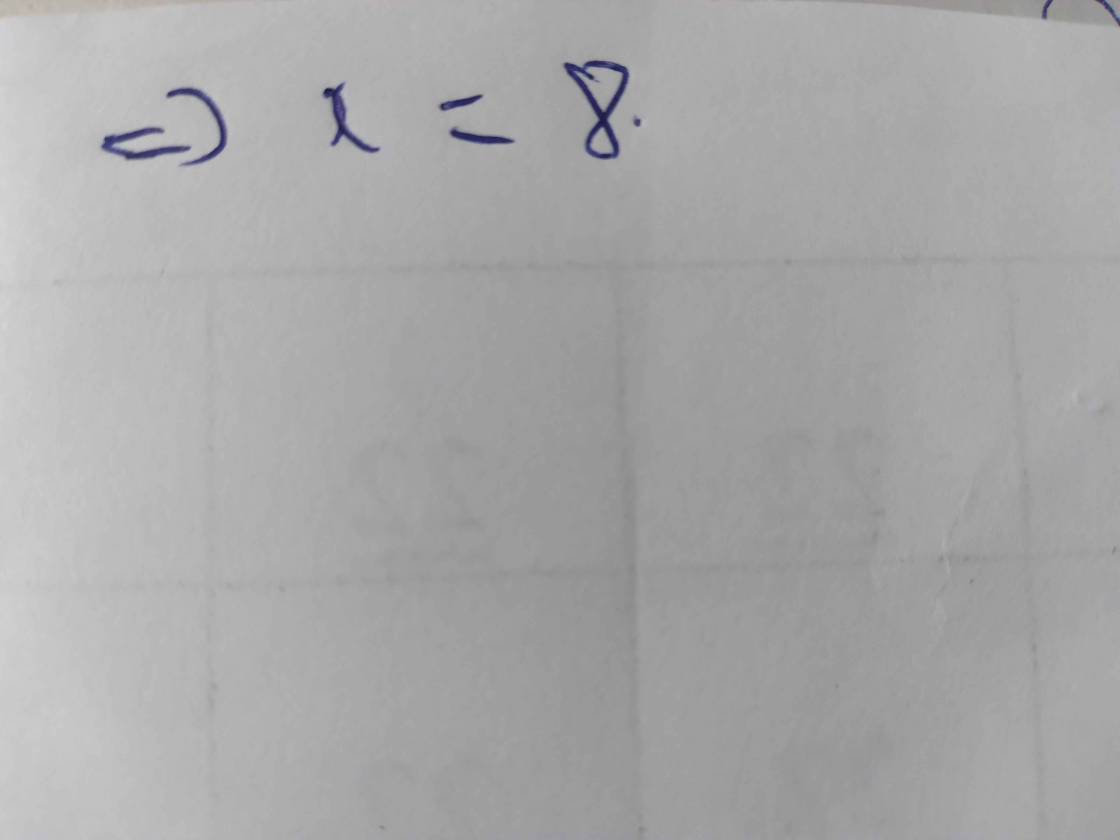
x=6
y=5
llllllllllllllllllllllllllllllllllll cho mk
Ta có 53xy : 5,9 và không chia hết cho 2
Ta có : các chữ số \(⋮\) 5 là các chữ số thuộc {0,5}
-Ta xét trường hợp y = 0
Khi y = 0 mà 5 + 3 + x + 0
Từ đó ta cs"
5 + 3 + x + 0 (thay y =0)
=> 8+x+0
=> x = 1 vì 8 + 1 = 9 \(⋮\)9 và có chữ số 0 ở cuối \(⋮\)5
Xét trường chữ số 5
Tương tự cách lí luận trên ta lại có phép tính:
5 + 3 + x + 5 (thay x =5)
=> 8+x+5
=>x=5 vì 8+5+5 = 13 + 5 =18 mà 18\(⋮\)9 và có chữ số 5 \(⋮\)5 nên x = 5 và y=5
=> X= {5,1}
Y={0,5}
=> 5310
=>5355