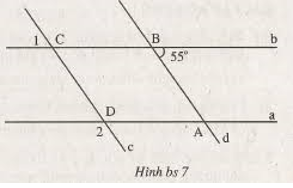
a, Hãy chỉ ra các cặp đường thẳng //. giải thích
b, Tính \(\widehat{C_1}\), \(\widehat{D_1}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc MAI+góc MEI=180 độ
=>MAIE nội tiếp
b: góc IEN+góc IBN=180 độ
=>IENB nội tiếp
=>góc ENI=góc EBI
góc MIN=góc MIE+góc NIE
=góc MAE+góc NBE
=90 độ-góc EAI+90 độ-góc EBI=90 độ

a) Ta có: đường thẳng a là đường trung trực của đoạn thẳng AB và CD nên \(a \bot AB;a \bot CD\).
Suy ra: AB // CD.
b) Đường thẳng a là đường trung trực của đoạn thẳng AB và CD nên MN là đường trung trực của đoạn thẳng AB và CD. Suy ra: MD = MC.
Xét tam giác vuông MNC và tam giác vuông MND có: ND = NC; MD = MC.
Vậy \(\Delta MNC = \Delta MND\)(cạnh huyền – cạnh góc vuông).
c) \(\Delta MNC = \Delta MND\)nên \(\widehat {CMN} = \widehat {DMN}\).
Mà \(\widehat {AMN} = \widehat {BMN} = 90^\circ \Rightarrow \widehat {AMN} - \widehat {DMN} = \widehat {BMN} - \widehat {CMN}\).
Vậy \(\widehat {AMD} = \widehat {BMC}\).
d) Xét hai tam giác AMD và BMC có:
MA = MB;
\(\widehat {AMD} = \widehat {BMC}\);
MD = MC.
Vậy \(\Delta MAD = \Delta MBC\)(c.g.c). Suy ra: \(AD = BC,\widehat A = \widehat B\) (cặp cạnh và góc tương ứng).
e) \(\Delta MAD = \Delta MBC\) nên \(\widehat {ADM} = \widehat {BCM}\) (2 góc tương ứng).
\(\Delta MNC = \Delta MND\) nên \(\widehat {MCN} = \widehat {MDN}\) (2 góc tương ứng).
Vậy \(\widehat {ADM} + \widehat {MDN} = \widehat {BCM} + \widehat {MCN}\) hay \(\widehat {ADC} = \widehat {BCD}\).

- Các đường thẳng cắt nhau khi có a ≠ a'. Ta có ba cặp đường thẳng cắt nhau là:
a) y = 1,5x + 2 và b) y = x + 2 (vì có 1,5 ≠ 1)
a) y = 1,5x + 2 và c) y = 0,5x – 3 (vì có 1,5 ≠ 0,5)
a) y = 1,5x + 2 và d) y = x – 3 (vì có 1,5 ≠ 1)
...v...v......v.....v.....
- Các đường thẳng song song khi có a = a' và b ≠ b'. Ta có các cặp đường thẳng song song với nhau là:
a) y = 1,5x + 2 và e) y = 1,5x – 1 (vì có 1,5 = 1,5 và 2 ≠ -1)
b) y = x + 2 và d) y = x – 3 (vì có 1 = 1 và 2 ≠ -3)
c) y = 0,5x – 3 và g) y = 0,5x + 3 (vì có 0,5 = 0,5 và -3 ≠ 3)