Tìm x
6 thuộc BC { 3;x }
Giúp mình vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án B
Phương trình đã cho tương đương với:
![]()
![]()
![]()
Xét hàm số f t = t 3 + 3 t trên ℝ
Tacó f ' t = 3 t 2 + 3 > 0 , ∀ t ∈ ℝ nên hàm số f t đồng biến trên ℝ
Suy ra
![]()
![]()
Xét hàm số g x = x + 1 x trên 1 2 ; 2
Ta có g ' x = 1 - 1 x 2
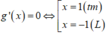
Bảng biến thiên:
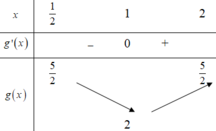
Dựa vào bảng biến thiên, để phương trình đã cho có hai nghiệm phân biệt trên 1 2 ; 2
⇔ Đường thẳng y = m cắt đồ thị hàm số g x = x + 1 x tại hai điểm phân biệt trên 1 2 ; 2
⇔ 2 < m ≤ 5 2

Đáp án D
Phương pháp:
Phương trình đã cho có nghiệm <=> đường thẳng y=m cắt đồ thị hàm số y = f x = 3 + x + 6 − x − 3 + x 6 − x tại ít nhất 1 điểm nên ta xét hàm f(x), từ đó tìm ra điều kiện của m.
Cách giải:
Xét hàm số: f x = 3 + x + 6 − x − 3 + x 6 − x trên − 3 ; 6
f ' x = 0 ⇔ 6 − x − 3 + x + 2 x − 3 = 0 ⇔ 3 − 2 x 6 − x − 3 + x − 3 − 2 x = 0 ⇔ x = 3 2 ∈ − 3 ; 6 6 − x − 3 + x = 1 *
* ⇔ 9 + 2 6 − x 3 + x = 1 ⇔ 2 6 − x 3 + x = − 8 (loại)
Ta có bảng biến thiên:
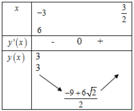
Vậy để phương trình f(x) có nghiệm thì: − 9 + 6 2 2 ≤ m ≤ 3

Biểu thức xác định khi x 2 - 36 ≠ 0 , x 2 + 6 x ≠ 0 , 6 – x ≠ 0 và 2x – 6 ≠ 0
x 2 - 36 ≠ 0 ⇒ (x – 6)(x + 6) ≠ 0 ⇒ x ≠ 6 và x ≠ -6
x 2 + 6 x ≠ 0 ⇒ x(x + 6) ≠ 0 ⇒ x ≠ 0 và x ≠ -6
6 – x ≠ 0 ⇒ x ≠ 6
2x – 6 ≠ 0 ⇒ x ≠ 3
Vậy x ≠ 0, x ≠ 3, x ≠ 6 và x ≠ -6 thì biểu thức xác định.
Ta có:
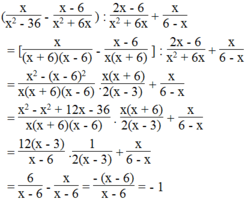
Vậy biểu thức không phụ thuộc vào biến x.