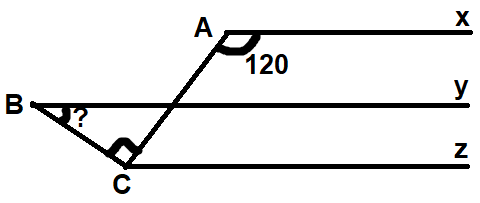
Đề bài:
Cho Ax // By , CAx = \(120^o\)và BCA = \(90^o\). Tính góc B.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NA
1
HQ
Hà Quang Minh
Giáo viên
24 tháng 7 2023
Kẻ tia Cz // Ax // By
Do Ax // Cz ⇒\(\widehat{CAx}+\widehat{ACz}=180^o\Rightarrow\widehat{ACz}+100^o=180^o\Rightarrow\widehat{ACz}=80^o\)
Mà \(\widehat{ACz}+\widehat{BCz}=\widehat{ACB}=25^o\)
⇒ By nằm giữa Cz và Ax
⇒ \(\widehat{BCz}=\widehat{ACz}-\widehat{BCA}=80^o-25^o=55^o\)
Mà Cz // By ⇒\(\widehat{CBy}+\widehat{BCz}=180^o\Rightarrow\widehat{CBy}=180^o-\widehat{BCz}=180^o-55^o=125^o\)
Còn góc \(\widehat{CDy}\) chưa thể tính được vì không có dữ liệu của D.
AT
29 tháng 6 2021
a) Ta có: \(OA=OB=OC=R\Rightarrow\Delta ABC\) vuông tại A
\(\Rightarrow\angle BAC=90\)
b) Vì \(OA=OB\Rightarrow\Delta OAB\) cân tại O \(\Rightarrow\angle OAB=\angle OBA\)
mà \(\angle BAx=\angle BCA\Rightarrow\angle BAx+\angle BAO=\angle BCA+\angle ABO\)
\(\Rightarrow\angle OAx=90\Rightarrow Ax\bot AO\Rightarrow Ax\) là tiếp tuyến của (O)
29 tháng 6 2021
a, - Ta có : BC là đường kính và \(A\in\left(O;R\right)\)
=> Tam giác ABC vuông tại A .
=> \(\widehat{BAC}=90^o\)
b, Ta có : \(\widehat{B}+\widehat{C}=90^o\)
Mà \(\left\{{}\begin{matrix}\widehat{B}=\widehat{BAO}\\\widehat{C}=\widehat{BCA}\end{matrix}\right.\)
\(\Rightarrow\widehat{BAC}+\widehat{BCA}=\widehat{OAx}=90^o\)
=> Ax vuông góc với bán kính .
=> Ax là tiếp tuyến ,
NT
1
HN
21 tháng 8 2021
Hình tự vẽ
Đặt N là giao điểm của AC và By
Vì Ax // By => ^CAx = ^CNy = 120 độ (Đồng vị)
Nên ^ACB + ^CBy = ^CNy (Góc ngoài tam giác NBC)
=> 60 độ + ^CBy = 120 độ
=> ^CBy = 60 độ
