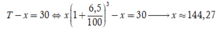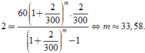ÔNG CHUYÊN DỰ ĐỊNH MUA 1 CHIẾC XE GẮN MÁY ĐỂ SỬ DỤNG .NGƯỜI BÁN HÀNG GIỚI THIỆU CHO ÔNG 2 LOẠI XE LÀ HONDA GIÁ 25 TRIỆU ,CHẠY ĐƯỢC 50KM/LÍT VÀ YAMAHA GIÁ 18TRIỆU CHẠY ĐƯỢC 40KM/LÍT .HỎI THEO EM ÔNG CHUYÊN NÊN MUA CHIẾC XE NÀO ? VÌ SAO ? BIẾT MỖI NGÀY ÔNG CHẠY 40KM VÀ GIÁ CỦA 1 LÍT XĂNG LÀ 20000 ĐỒNG