Cho hình dưới, biết a // b. Hãy tính số đo của góc AOB
A B O a b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
31 tháng 5 2019
Qua O kẻ đường thẳng c // a // b.
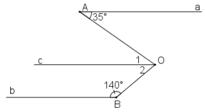
Vì a//c nên ∠A = ∠(O1) (hai góc so le trong)
Mà ∠A = 35o nên ∠(O1) = 35o
Vì b // c nên ∠(O2) + ∠B = 180o (hai góc trong cùng phía bù nhau)
⇒ ∠(O2) = 180o - ∠B
Mà ∠B = 140o ⇒ ∠(O2) = 180o – 140o = 40o
x = ∠(AOB) = ∠(O1) + ∠(O2) = 35o + 40o = 75o.
MT
0
NT
0
K
13 tháng 7 2019
a. Ta thực hiện, như sau:
- Vẽ \(MP\perp Ox,\)rồi lấy trên tia MP điểm A sao cho PA = PM.
- Vẽ \(MQ\perp Oy,\)rồi lấy trên tia MQ điểm B sao cho QB = QM.
b. Ta có:
- Vì OP là trung trực của AM nên OM = OA.(1)
- Vì OQ là trung trực của BM nên OM = OB.(2)
Từ (1),(2) suy ra:
\(OA=OB\Leftrightarrow O\)thuộc đường trung trực của AB.
c. Nhận xét về các cặp tam giác vuông có chung một cạnh và một cạnh khác bằng nhau, ta có:
\(\Delta POA=\Delta POM\Rightarrow\widehat{O_1}=\widehat{O_2};\Delta QOB=\Delta QOM\Rightarrow\widehat{O_3}=\widehat{O_4}\)
Ta có:
\(\widehat{xOy}=\widehat{O_2}+\widehat{O_3}.\)
\(\widehat{AOB}=\widehat{O_1}+\widehat{O_2}+\widehat{O_3}+\widehat{O_4}=\left(\widehat{O_1}+\widehat{O_4}\right)+\left(\widehat{O_2}+\widehat{O_3}\right)\)
\(=\left(\widehat{O_2}+\widehat{O_3}\right)+\left(\widehat{O_2}+\widehat{O_3}\right)=2\left(\widehat{O_2}+\widehat{O_3}\right)=2\widehat{xOy}=2\alpha.\)
d. Nếu \(\widehat{xOy}=90^o\)thì:
\(\widehat{AOB}=2.90^o=180^o\Leftrightarrow A,O,B\)thẳng hàng <=> O là trung điểm của AB.
13 tháng 1 2022
a: Số đo cung nhỏ là 120 độ
Số đo cung lớn là 360-120=240(độ)
b: Xét ΔOAB có OA=OB
nên ΔOAB cân tại O
Suy ra: \(\widehat{OAB}=\widehat{OBA}=\dfrac{180^0-120^0}{2}=30^0\)
4 tháng 7 2016
c) Chọn 1 tia bất kì, từ tia đó kẻ tới n - 1 tia còn lại ta đc n - 1 góc mà có tất cả n tia => có: n.(n - 1) góc nhưng như vậy số góc đã đc tính 2 lần => số góc thực tế là: n.(n - 1)/2 = 171 (góc)
=> n.(n - 1) = 171 x 2
=> n.(n - 1) = 18.19
=> n = 19
... bn tự lm típ, đến đây thì dễ rùi
Ủng hộ mk nha ^_-
6 tháng 7 2016
c) Chọn 1 tia bất kì, từ tia đó kẻ tới n - 1 tia còn lại ta đc n - 1 góc mà có tất cả n tia => có: n.(n - 1) góc nhưng như vậy số góc đã đc tính 2 lần => số góc thực tế là: n.(n - 1)/2 = 171 (góc)
=> n.(n - 1) = 171 x 2
=> n.(n - 1) = 18.19
=> n = 19