Bài 1: Qui đồng mẫu các phân thức sau:
a) \(\frac{3}{2x-6};\frac{1}{3x-6}\)
b) \(\frac{1}{2x^2-8x+8};\frac{1}{3\left(x-2\right)};\frac{1}{x^2-x-2}\)
Giúp đỡ e vs mn :((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) + Phân tích mẫu thức thành nhân tử để tìm nhân tử chung:
x3 – 1 = (x – 1)(x2 + x + 1)
x2 + x + 1 = x2 + x + 1
⇒ MTC = (x – 1)(x2 + x + 1) = x3 – 1
+ Nhân tử phụ : (Có thể bỏ qua bước này nếu đã quen)
(x3 – 1) : (x3 – 1) = 1
(x3 – 1) :( x2 + x + 1) = x - 1
(x3 – 1) : 1 = x3 – 1
+ Quy đồng :
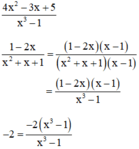
b) Ta có:
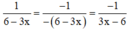
+ Phân tích mẫu thức thành nhân tử để tìm MTC
x + 2 = x + 2
2x – 4 = 2.(x – 2)
3x – 6 = 3.(x – 2)
⇒ MTC = 6.(x + 2)(x – 2)
+ Nhân tử phụ: (Có thể bỏ qua bước này nếu đã quen)
6(x + 2)(x – 2) : (x + 2) = 6(x – 2)
6(x + 2)(x – 2) : 2(x – 2) = 3(x + 2)
6(x + 2)(x – 2) : 3(x – 2) = 2(x + 2)
+ Quy đồng:
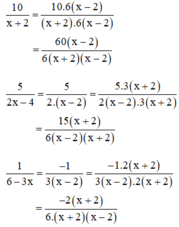

Ta có \(\frac{2}{x^3-y^3}=\frac{2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(\frac{2x-1}{x^2-y^2}=\frac{2x+1}{\left(x+y\right)\left(x-y\right)}\)
\(\frac{1}{x+y}\) giữ nguyên
MTC: \(\left(x+y\right)\left(x-y\right)\left(x^2+xy+y^2\right)\)
Các nhân tử phụ tương ứng là : \(\left(x+y\right);\left(x-y\right)\left(x^2+xy+y^2\right);\left(x^2+xy+y^2\right)\)
Ta có:
\(\frac{2}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\frac{2.\left(x+y\right)}{\left(x-y\right)\left(x+y\right)\left(x^2+xy+y^2\right)}\)
\(\frac{1}{x+y}=\frac{1.\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(x+y\right)\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(\frac{2x+1}{\left(x+y\right)\left(x-y\right)}=\frac{\left(2x+1\right)\left(x^2+xy+y^2\right)}{\left(x+y\right)\left(x-y\right)\left(x^2+xy+y^2\right)}\)

\(\frac{x+2}{4x-x^2-3}=\frac{-\left(x+2\right)}{x^2-4x+3}=\frac{\left(-x-2\right)\left(2x+5\right)}{\left(x-1\right)\left(x-3\right)\left(2x+5\right)}=\frac{-2x^2-9x-10}{\left(x-1\right)\left(x-3\right)\left(2x+5\right)}\)
\(\frac{1}{2x^2+3x-5}=\frac{1}{\left(x-1\right)\left(2x+5\right)}=\frac{x-3}{\left(x-1\right)\left(x-3\right)\left(2x+5\right)}\)