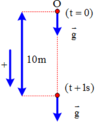
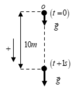
Từ trên độ cao của một tòa nhà cao tầng , người ta thả rơi tự do một vật A . Một giây sau , ở tầng thấp hơn 10 m , dọc theo phương chuyển động của vật A người ta buông rơi vật B . lấy g = 10 m/s2 .
a) sau bao lâu hai vật A và B sẽ đụng nhau ? tính vận tốc của hai vật đó và quãng đường mà vật B đã đi được .
b) tính khoảng cách giữa hai vật A và B sau 2s kể từ lúc vật A bắt đầu rơi...
Đọc tiếp
Từ trên độ cao của một tòa nhà cao tầng , người ta thả rơi tự do một vật A . Một giây sau , ở tầng thấp hơn 10 m , dọc theo phương chuyển động của vật A người ta buông rơi vật B . lấy g = 10 m/s2 .
a) sau bao lâu hai vật A và B sẽ đụng nhau ? tính vận tốc của hai vật đó và quãng đường mà vật B đã đi được .
b) tính khoảng cách giữa hai vật A và B sau 2s kể từ lúc vật A bắt đầu rơi .
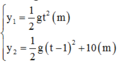
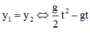
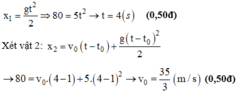
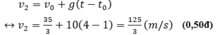
(0,5 điểm)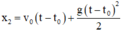
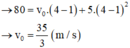(0,5 điểm)
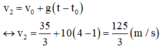(0,5 điểm)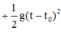
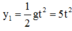
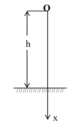
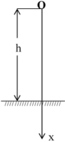
Chọn trục Oy, gốc O đặt tại vị trí thả vật A,chiều dương hướng xuống
Các phương trình tọa độ :
\(\left\{{}\begin{matrix}y_1=\frac{1}{2}gt^2\left(m\right)\\y_2=\frac{1}{2}g\left(t-1\right)^2+10\left(m\right)\end{matrix}\right.\)
Khi đụng nhau : y2=y1
\(\frac{gt^2}{2}-gt+\frac{1}{2}g+10=\frac{gt^2}{2}\)
=> t =1,5s
Quãng đường rơi của 2 vật :
\(s_1=\frac{1}{2}gt^2=\frac{1}{2}.10.1,5^2=11,25m\)
\(s_2=\frac{1}{2}g\left(t-1\right)^2=1,25m\)
Vận tốc của 2 vật :
\(v_1=\sqrt{2.10.11,25}=15m/s\)
\(v_2=\sqrt{2.10.1,25}=5m/s\)
b) Kể từ khi A rơi:
\(s_A=\frac{1}{2}gt^2=20m\)
\(s_B=\frac{1}{2}g\left(t-1\right)^2=5m\)
t =2s => \(\Delta s=s_A-s_B=20-5=15m\)