1/(d): y=ax+b vuông góc (d') : x-2x+3=0 và cắt Oy tại điểm có tung độ là -3
2/(d) song song (d'):y=-2x-3 và cắt Ox tại điểm có hoành độ là 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 8 2015
Vì đường thẳng d song song hoặc trùng với đường thẳng d1 : y = ax; đường thẳng d': y = a'x + b' song song hoặc trùng với đường thẳng d2 :
y = a'x nên Nếu d vuông góc với d' thì d1 vuông góc với d2
Nhận xét: d1 và d2 đều đi qua gốc O mà d1 vuông góc với d2 nên có 1 đường thẳng nằm trong góc phần tư thứ I và III ( giả sử là d1) ; đường thẳng còn lại nằm trong góc phần tư thứ II và IV . => a > 0 và a' < 0
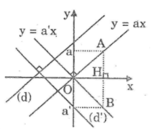
O y x d 1 d 2 H A B
Lấy H (1; 0). Qua H kẻ đường vuông góc với Ox cắt d1; d2 lần lượt tại B ; A
=> xA = xB = 1
A thuộc d2 => yA = a' ; B thuộc d1 => yB = a
=> HA = |a'|; HB = |a|
Áp dụng hệ thức lượng trong tam giác vuông AOB có: OH2 = HA . HB => 1 = |a|. |a'| => |a.a'| = 1 => a.a' = - 1 ( Vì a;a' trái dấu nên a.a' < 0)
Vậy....
24 tháng 9 2021
\(a,\left(d\right).qua.A\left(1;-3\right)\Leftrightarrow x=1;y=-3\\ \Leftrightarrow a+b=-3\left(1\right)\\ \left(d\right).qua.B\left(1;4\right)\Leftrightarrow x=1;y=4\\ \Leftrightarrow a+b=4\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow a,b.vô.nghiệm\)
\(b,\left(d\right).qua.A\left(-1;2\right)\Leftrightarrow x=-1;y=2\Leftrightarrow-a+b=2\\ \left(d\right)//\left(d'\right)\Leftrightarrow\left\{{}\begin{matrix}a=-7\\b\ne2021\end{matrix}\right.\Leftrightarrow-7+b=2\Leftrightarrow b=9\)
\(c,\left(d\right).qua.A\left(2;1\right)\Leftrightarrow x=2;y=1\Leftrightarrow2a+b=1\\ \left(d\right)\perp\left(d'\right)\Leftrightarrow a\cdot3=-1\Leftrightarrow a=-\dfrac{1}{3}\\ \Leftrightarrow-\dfrac{2}{3}b=1\Leftrightarrow b=-\dfrac{3}{2}\)
CM
17 tháng 2 2019
Qua gốc tọa độ, kẻ đường thẳng y = ax // (d) và y = a’x // (d’)
*Chứng minh (d) vuông góc với (d’) thì a.a’ = -1
Không mất tính tổng quát, giả sử a > 0
Khi đó góc tạo bởi tia Ox và đường thẳng y = ax là góc nhọn.
Suy ra góc tạo bởi tia Ox và đường thẳng y = a’x là góc tù (vì các góc tạo bởi đường thẳng y = ax và đường thẳng y = a’x với tia Ox hơn kém nhau 900).
Suy ra: a’ < 0
Mà đường thẳng y = ax đi qua A(1; a), đường thẳng y = a’x đi qua B(1; a’) nên đoạn AB vuông góc với Ox tại điểm H có hoành độ bằng 1.
Vì (d) ⊥ (d’) nên hai đường thẳng y = ax và y = a’x vuông góc với nhau. Suy ra: góc(AOB) = 90 °
Tam giác vuông AOB có OH ⊥ AB. Theo hệ thức lượng trong tam giác vuông, ta có: OH2 = HA.HB
Hay: a.|a’| = 1 ⇔ a.(-a’) = 1 ⇔ a.a’ = -1
Vậy nếu (d) vuông góc với (d’) thì a.a’ = -1
*Chứng minh a.a’ = -1 thì (d) vuông góc với (d’)
Ta có: a.a’ = -1 ⇔ a.|a’| = 1 hay HA.HB = O H 2
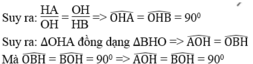
Suy ra OA ⊥ OB hay hai đường thẳng y = ax và y = a’x vuông góc với nhau hay (d) ⊥ (d’)
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Phương trình tổng quát của đường thẳng \(d,d'\) lần lượt là: \(ax - y + b = 0,{\rm{ }}a'x - y + b' = 0\).
Do đó \(\overrightarrow {{n_d}} = \left( {a; - 1} \right),{\rm{ }}\overrightarrow {{n_{d'}}} = \left( {a'; - 1} \right)\).
Ta có \(d \bot d' \Leftrightarrow \overrightarrow {{n_d}} \bot \overrightarrow {{n_{d'}}} \Leftrightarrow \overrightarrow {{n_d}} .\overrightarrow {{n_{d'}}} = 0 \Leftrightarrow a.a' + \left( { - 1} \right)\left( { - 1} \right) = 0 \Leftrightarrow a.a' = - 1\).
14 tháng 12 2020
a) Vì đồ thị hàm số y=ax+b vuông góc với đồ thị hàm số \(y=\dfrac{1}{3}x-1\) nên \(a\cdot\dfrac{1}{3}=-1\)
\(\Leftrightarrow a=-1:\dfrac{1}{3}=-1\cdot\dfrac{3}{1}=-3\)
Vậy: Hàm số có dạng y=-3x+b
Vì đồ thị hàm số y=-3x+b đi qua điểm A(1;2) nên
Thay x=1 và y=2 vào hàm số y=-3x+b, ta được:
\(-3\cdot1+b=2\)
\(\Leftrightarrow b-3=2\)
hay b=5
Vậy: Hàm số có dạng y=-3x+5
13 tháng 12 2020
a) Vì đồ thị hàm số ax+b song song với (d1) nên a=3
hay hàm số có dạng là y=3x+b
Vì đồ thị hàm số y=3x+b đi qua điểm C(3;-2)
nên Thay x=3 và y=-2 vào hàm số y=3x+b, ta được:
\(3\cdot3+b=-2\)
\(\Leftrightarrow b+9=-2\)
hay b=-11
Vậy: Hàm số có dạng là y=3x-11
b) Vì (d)⊥(d2) nên \(a\cdot4=-1\)
hay \(a=-\dfrac{1}{4}\)
Vậy: Hàm số có dạng là \(y=-\dfrac{1}{4}x+b\)
Vì (d) đi qua D(2;-1) nên
Thay x=2 và y=-1 vào hàm số \(y=-\dfrac{1}{4}x+b\), ta được:
\(-\dfrac{1}{4}\cdot2+b=-1\)
\(\Leftrightarrow b-\dfrac{1}{2}=-1\)
hay \(b=-\dfrac{1}{2}\)
Vậy: \(a=-\dfrac{1}{4}\) và \(b=-\dfrac{1}{2}\)
1/ Bạn viết ko đúng pt của (d')
2. Theo bài ra ta có:
\(\left\{{}\begin{matrix}a=-2\\2.a+b=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=4\end{matrix}\right.\) \(\Rightarrow y=-2x+4\)