Cho A = 3+32+33+...+32008.Tìm x biết : 2A+3=3x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 8 2023
`@` `\text {Ans}`
`\downarrow`
`A = 3 + 3^2 + ... + 3^99 + 3^100`
`=> 3A = 3^2 + 3^3 + ... + 3^100 + 3^101`
`=> 3A - A = (3^2 + 3^3 + ... + 3^100 + 3^101) - (3 + 3^2 + ... + 3^99 + 3^100)`
`=> 2A = 3^101 - 3`
`=> 2A + 3 = 3^101 + 3 - 3`
`=> 2A + 3 = 3^101`
Ta có:
`2A + 3 = 3^x`
`=> x = 101.`
7 tháng 8 2023
A=3+3^2+...+3^100
=>3*A=3^2+3^3+...+3^101
=>2A=3^101-3
=>2A+3=3^101
Theo đề, ta có: 3^x=3^101
=>x=101
OY
20 tháng 7 2021
A=3+32+33+...+3100
3A=32+33+...+3101
3A-A=(32+33+...+3101)-(3+32+33+...+3100)
2A=3101-3
2A+3=3101
DX
20 tháng 7 2021
\(A=3+3^2+3^3+...+3^{100}\)
\(\Rightarrow3A=3.\left(3+3^2+3^3+...+3^{100}\right)\)
\(\Rightarrow3A=3^2+3^3+3^4+...+3^{101}\)
\(\Rightarrow3A-A=2A=\left[3^2+3^3+3^4+...+3^{101}\right]-\left[3+3^2+3^3+...+3^{100}\right]\)\(\Rightarrow2A=3^{101}-3\)
Theo đề bài ta có 2A + 3 = 3n ( \(n\in N\) )
\(\Rightarrow2A+3=3^{101}-3+3=3^n\)
\(\Rightarrow2A+3=3^{101}=3^n\)
\(\Rightarrow3^{101}=3^n\)
\(\Rightarrow101=n\) ( thỏa mãn điều kiện \(n\in N\)
Vậy n = 101
PT
1
CM
22 tháng 11 2018
Ta có: A = 3 + 3 2 + 3 3 + . . . + 3 100
=> 3 A = 3 2 + 3 3 + 3 4 + . . . + 3 101
=> 3 A - A = ( 3 2 + 3 3 + 3 4 + . . . + 3 101 ) - ( 3 + 3 2 + 3 3 + . . . + 3 100 )
=> 2 A = 3 2 + 3 3 + 3 4 + . . . + 3 101 - 3 - 3 2 - 3 3 - . . . - 3 100
2 A = 3 101 - 3 <=> 2 A + 3 = 3 101 , mà 2 A + 3 = 3 n
=> n = 101
TN
2
OY
13 tháng 8 2021
A=3+32+33+...+399
3A=32+33+...+3100
3A-A=(32+33+...+3100)-(3+32+33+...+399)
2A=3100-3
2A+3=3100
⇒n=100
BS
13 tháng 8 2021
Đây nè bạn, chúc bạn học tốt :))
A = 3 + 32 + 33+ ... + 399
3A = 3. (3 + 32 + 33+ ... + 399)
3A \(=3^2+3^3+3^4+...+3^{100}\)
3A \(=\left(3^2+3^3+3^4+...+3^{100}\right)-\left(3+3^2+3^3+...+3^{99}\right)\)
2A\(=3^{100}-3\)
Vậy, sau khi tìm đc 2A, ta tìm stn n nha:
2A + 3 = 3n
\(=3^{100}-3+3=3^n\)
⇒\(3^{100}=3^n\)(Vì -3 +3 = 0)
Vậy n = 100
MS
1
CM
22 tháng 6 2017
a, A = 3 + 3 2 + 3 3 + . . . + 3 12 => 3A = 3 2 + 3 3 + . . . + 3 13
=> 3A - A = ( 3 2 + 3 3 + . . . + 3 13 ) - ( 3 + 3 2 + 3 3 + . . . + 3 12 )
=> 2A = 3 13 - 3 => A = 3 13 - 3 2
Vì A = 3 x - 3 2 => x = 13 => x+2016 = 2029
b, Số tập hợp con của tập A có x phần tử là 2 x
=> 2 x = 64 = 2 6 => x = 6. Vậy tập A có 6 phần tử
2 tháng 10 2021
a: Tổng các số hạng là:
\(\dfrac{\left(220+1\right)\cdot220}{2}=24310\)
Ta có: A+1=2x
\(\Leftrightarrow2x=24311\)
hay \(x=\dfrac{24311}{2}\)
18 tháng 6 2018
a,
A = 1 + 3 + 32 + 33 + ... + 3119
3A = 3.(1 + 3 + 32 + 33 + ... + 3119)
3A = 3 + 32 + 33 + 34+ ... + 3120
2A = 3A - A = (3 + 32 + 33 + 34 + ... + 3120) - (1 + 3 + 32 + 33 + ... + 3119)
2A = 3120 - 1
A = \(\frac{3^{120}-1}{2}\)
Vậy A = \(\frac{3^{120}-1}{2}\)
b, Ta có : 3120 - 1 + 1 = 27x
<=> 3120 = 27x
<=> 3120 = (33)x
<=> 3120 = 3x
<=> x = 120
Vậy x = 120
c, A có chia hết cho 5 và 13
19 tháng 6 2018
Sua cho \(\left(3^3\right)^x=3^{3x}\) nha
\(\Rightarrow3^{120}=3^{3x}\Rightarrow x=\frac{120}{3}=40\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
24 tháng 12 2022
a, A = 1 + 3 + 32 + 33 +....+32022
3A = 3 + 32 + 33 +.....+32022 + 32023
3A - A = 32023 - 1
2A = 32023 - 1
2A - 22023 = 32023 - 1 - 22023
2A - 22023 = -1
b, x \(\in\) Z và x + 10 \(⋮\) x - 1 ( đk x# 1)
x + 10 \(⋮\) x - 1
\(\Leftrightarrow\) x - 1 + 11 \(⋮\) x - 1
11 \(⋮\) x - 1
x-1 \(\in\) { -11; -1; 1; 11}
x \(\in\) { -10; 0; 2; 12}
Kết luận các số nguyên x thỏa mãn yêu cầu đề bài là :
x \(\in\) { -10; 0; 2; 12}
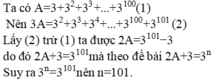
Ta có: \(A=3+3^2+3^3+...+3^{2008}\)
\(3A=3^2+3^3+3^4+...+3^{2009}\)
\(3A-A=3^{2009}-3\)
Hay \(2A=3^{2009}-3\)
\(\Rightarrow2A+3=3^x\)
\(\Rightarrow\left(3^{2009}-3\right)+3=3^x\)
\(\Rightarrow3^{2009}=3^x\)
\(\Rightarrow x=2009\)
Hok tốt nha^^
Có A=3+32+...+32008
=>3A=32+33+...+32009
=>3A-A=2A=32009-3
Thay 2A vào 2A+3=3x
Ta được: 32009-3+3=3x
=>32009=3x
=>x=2009
Vậy..