diện tích tam giác đều ABC ngoại tiếp đường tròn tâm I có bán kính \(\sqrt[4]{3}\) thì diện tích tam giác ABC bằng bao nhiêu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 1 2016
bán kính là a đi chẳng hạn
Vì tam giác đều ABC ngoại tiếp đường tròn I nên đcao AH bằng đường kính => AH = 2a
Vì tam giác ABC đều nên BC = AB = AH / sinB = a / sin60o =2a/ căn 3 (hai a chia căn ba)
Diện tích ABC = 1/2. AH. BC= 1/2. 2a . (2a/ căn 3) =2x2 / căn 3
Đáp án bài toán trên là Sabc = 2
CM
26 tháng 7 2019
- Chọn D.
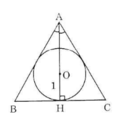
- Gọi O là tâm đường tròn nội tiếp Δ ABC, H là tiếp điểm thuộc BC.
Đường phân giác AO của góc A cũng là đường cao nên A, O, H thẳng hàng.
Ta có: HB = BC, ∠HAC = 30o, AH = 3.OH = 3 (cm)
9 tháng 12 2015
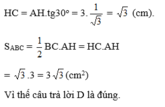
biết là bằng 9 rồi nhưng mà (Nhập kết quả dưới dạng số thập phân gọn nhất)
tính sao?????
CM
9 tháng 7 2019
- Chọn D.
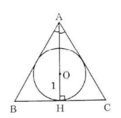
- Gọi O là tâm đường tròn nội tiếp Δ ABC, H là tiếp điểm thuộc BC.
Đường phân giác AO của góc A cũng là đường cao nên A, O, H thẳng hàng.
Ta có: HB = BC, ∠HAC = 30o, AH = 3.OH = 3 (cm)
12 tháng 1 2016
bài này dễ mà
có nhiêu cách tính lắm
mik sẽ trình bày một cách nha !!!
gọi O là tâm của đường tròn ngoại tiếp tam giác ABC
ta có : tam giác ABC cân taỊ A
mà AO= 1/2 BC=\(3\sqrt{2}\)
nên AO là đường trung tuyến của tam giác ABC
ĐỒNG THỜI CŨNG LÀ ĐƯỜNG cao của tam giác ABC
ta lại có : BC=2R=2*\(3\sqrt{2}\)=6\(\sqrt{2}\)
S của tam giác ABC= 1/2 *AO*BC=1/2*\(3\sqrt{2}\cdot6\sqrt{2}\)=18
vậy diện tich tam giác là 18
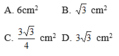
h = 3 R =3\(\sqrt{3}\) ( vì đường cao đồng thời là trung tuyens)
mà h =\(\frac{a\sqrt{3}}{2}\)
=> a =\(\frac{6R}{\sqrt{3}}=6\)
=> S =ah/2 =.6.3.\(\sqrt{3}\)/2 = 9 \(\sqrt{3}\)