Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tham khảo:
(vì góc BOD là góc ngoài)
(Do BO,CO là các tia phân giác của tam giác ABC)
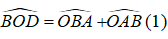
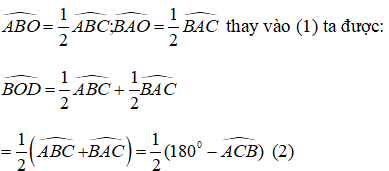
a/ Vì \(\widehat{B}=\widehat{C}\)(gt)
mà BD, CE là tia p.g của \(\widehat{B},\widehat{C}\)
\(\Rightarrow\widehat{ABD}=\widehat{DBC}=\widehat{ACE}=\widehat{ECB}\)
Xét tam giác BCD và tam giác CBE ta có:
\(\hept{\begin{cases}\widehat{B}=\widehat{C}\\BC:canh\\\widehat{DBC}=\widehat{ECB}\left(gt\right)\end{cases}}chung\)
suy ra tam giác BCD bằng tam giác CBE ( c.g.c )
Nhớ k cho mình nhé! Thank you!!!
b/ Vì \(\widehat{OBC}=\widehat{OCB}\left(cmt\right)\)
suy ra tam giác OBC cân tại O
suy ra OB = OC
Nhớ k cho mình nhé! Thank you!!!
Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
cau 1 :
Xet tam giac ABD va tam giac EBD co : BD chung
goc ABD = goc DBE do BD la phan giac cua goc ABC (gt)
AB = BE (Gt)
=> tam giac ABD = tam giac EBD (c - g - c)
=> goc BAC = goc DEB (dn)
ma goc BAC = 90 do tam giac ABC vuong tai A (gt)
=> goc DEB = 90
=> DE _|_ BC (dn)
b, tam giac ABD = tam giac EBD (cau a)
=> AB = DE (dn)
AB = 6 (cm) => DE = 6 cm
DE _|_ BC => tam giac DEC vuong tai E
=> DC2 = DE2 + CE2 ; DC = 10 cm (gt); DE = 6 cm (cmt)
=> CE2 = 102 - 62
=> CE2 = 64
=> CE = 8 do CE > 0
a) xét tam giác ABD và tam giác ACD có
AB=AC,AD là cạnh chung góc BAD= góc DAC
vậy tam giác ABD=tam giác ACD(C.g.c)
Suy ra gócADB=gócADC=1/2BDC=1/2*180=90
Hay AD vuông góc với BC
Moọe,làm xong tự nhiên olm tải lại tap.
Vẽ giùm cái hình (hồi nãy vẽ hình đẹp lắm mà giờ bị mất->lười vẽ)
a)Xét tam giác DMB và AME có:
\(\hept{\begin{cases}MA=MD\left(gt\right)\\\widehat{AME}=\widehat{DMB}\left(đđ\right)\\BM=EM\left(gt\right)\end{cases}}\Rightarrow\Delta DMB=\Delta AME\Rightarrow AE=BD\)
b)Từ \(\Delta DMB=\Delta AME\Rightarrow\widehat{MDB}=\widehat{MAE}=90^o\Rightarrow AE//BD\) (so le trong) (1)
Đến đây chứng minh FA // DC bằng cách chứng minh tam giác AMF = tam giác DMC để suy ra góc CMD = góc AMF = 90o (so le trong)
Từ đó suy ra E;A;F thẳng hàng.
a: góc BEC=góc BFC=90 độ
=>BFEC nội tiếp
=>góc BFE+góc BCE=180 độ
=>góc AFE=góc ACB
b: Xét ΔABD và ΔANC có
góc ABD=góc ANC
góc BAD=góc NAC
=>ΔABD đồng dạng với ΔANC
=>AB/AN=BD/NC
=>AB*NC=AN*BD
