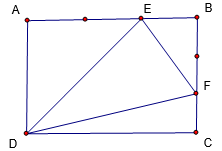
Cho hình chữ nhật ABCD có diện tích 144cm2 . Trên AB lấy điểm E , trên BC lấy điểm F . Các đoạn EB 1 3 AB , CF 1 3 CB . Tính diện tích hình tam giác DEF.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
29 tháng 9 2019
Gọi độ dài AB là a,độ dài BC là b thì S(ABCD)=ab=144
S(ABE)+S(ECF)+S(ADF)+S(AEF)=S(ABCD)
<=> 1/2AB.BE+1/2EC.CF+1/2AD.DF+S(AEF)=AB.BC
<=>1/2a.2/3b+1/2b/3.2/3a+1/2b.a/3+S(AEF)=a.b
<=>ab/3+ab/9+ab/6+S(AEF)=ab
<=>S(AEF)=7/18ab=56
LA
10 tháng 1 2018
3) Ta có: Trung điểm ở giữa đoạn thẳng
Vậy chiều cao tam giác NMC là :
4:2=2 (cm)
Đáy tam giác NMC tương tự như trên
Đáy NMC bằng 1 nữa đoạn thẳng AB
6:2=3(cm)
Diện tích tam giác NMC :
3x2:2=3(cm2)
Đoạn AB cũng là đáy cũng là đáy tam giác ABM
Vậy đáy tam giác ABM là 6cm
Chiều cao tam giác ABM bằng 1 nữa đoạn BC (tính chiều cao tgiác NMC ta dc 2cm,vì trung điểm ở giữa 2 đoạn BC
Chiều cao tam giác ABM là :
4-2=2(cm)
Diện tích tam giác ABM là :
6x2:2=6(cm2)
Chiều cao tam giác DAN=chiều rộng hcn ABCD nên chiều cao là: 4cm
Đáy tam giác DAN bằng chiều dài hcn ABCD
Đáy dài:
6:2=3(cm)
Diện tích tam giác DAN :
4x3:2=6(cm2)
Diện tích hcn ABCD :
6x4=24(cm2)
Diện tích tam giác AMN :
24-6-2-6=10(cm2)
Đs:...
KT
10 tháng 1 2018
1) \(S_{ABC}=\frac{AB.AC}{2}=\frac{3\times4}{2}=6\left(cm^2\right)\)
2) a) \(S_{EDC}=\frac{AD\times DC}{2}=\frac{3\times4}{2}=6\left(cm^2\right)\) (vì chiều cao hạ từ E xuống DC = chiều rộng của hình chữ nhật)
b) \(S_{AED}+S_{EBC}=\frac{AE\times AD}{2}+\frac{EB\times BC}{2}\)
\(=\frac{AE\times AD+EB\times AD}{2}\) (vì BC = AD)
\(=\frac{AD\times\left(AE+EB\right)}{2}=\frac{3\times4}{2}=6\left(cm^2\right)\)