Phương trình \(\sqrt{3}tan2x+3=0\) có bao nhiêu nghiệm thuộc khoảng (2000pi; 2018pi)
Mọi người giúp em cách lấy nghiệm khi cho pi lớn thế này với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 10 2018
Chọn D
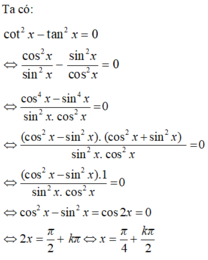
Vậy trong khoảng (0,2π), phương trình có các nghiệm là π 4 ; 3 π 4 ; 5 π 4 ; 7 π 4 nên tổng các nghiệm là 4π
17 tháng 7 2021
Pt \(\Leftrightarrow2sin\left(2x+\dfrac{\pi}{3}\right)=\sqrt{3}\)
\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=k\pi\end{matrix}\right.\)\(\left(k\in Z\right)\)
\(x\in\left(0;\dfrac{\pi}{2}\right)\)\(\Rightarrow\left[{}\begin{matrix}0< \dfrac{\pi}{6}+k\pi< \dfrac{\pi}{2}\\0< k\pi< \dfrac{\pi}{2}\end{matrix}\right.\)\(\left(k\in Z\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}-\dfrac{1}{6}< k< \dfrac{1}{3}\\0< k< \dfrac{1}{2}\end{matrix}\right.\)\(\left(k\in Z\right)\)\(\Leftrightarrow\left[{}\begin{matrix}k=0\\k\in\varnothing\end{matrix}\right.\)
Vậy có 1 nghiệm thỏa mãn
PT
1
CM
2 tháng 5 2018
Đáp án C
PT 2 x = − π 4 + k 2 π 2 x = 5 π 4 + k 2 π ⇔ x = − π 8 + k π x = 5 π 8 + k π k ∈ ℤ
Vì x ∈ 0 ; π ⇒ 0 < − π 8 + k π < π 0 < 5 π 8 + k π < π ⇔ 1 8 < k < 9 8 − 5 8 < k < 3 8 ⇒ k = 1 k = 0 ⇒ x = 7 π 8 x = 5 π 8
\(tan2x=-\sqrt{3}=tan\left(-\frac{\pi}{3}\right)\)
\(\Rightarrow2x=-\frac{\pi}{3}+k\pi\Rightarrow x=-\frac{\pi}{6}+\frac{k\pi}{2}\)
Do \(x\in\left(2000\pi;2018\pi\right)\)
\(\Rightarrow2000\pi< -\frac{\pi}{6}+\frac{k\pi}{2}< 2018\pi\)
\(\Rightarrow4001\le k\le4036\) (đã làm tròn đến phần nguyên)
\(\Rightarrow\) có 36 giá trị
Trên thực tế, với các hàm lượng giác thì miền \(\left(2000\pi;2018\pi\right)\) ko khác gì miền \(\left(0;18\pi\right)\) cả, bạn tính trên \(\left(0;18\pi\right)\) kết quả cũng sẽ y hệt
có cách nào giải nhanh hơn k bạn ơi