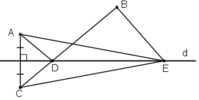
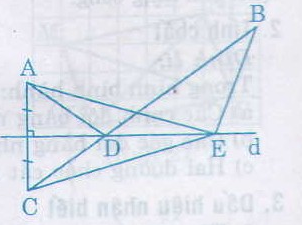
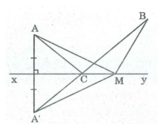
Cho hai điểm A, B thuộc cùng một nửa mặt phẳng bờ là đường thẳng d. Gọi C là điểm đối xứng với A qua d. Gọi D là giao điểm của đường thẳng d là đoạn thẳng BC. Gọi E là điểm bất kì của đường thẳng d (E khác D).
Chứng minh rằng AD + DB < AE + EB
Trong một lần lên giải bài tập: Em giải như sau:
A C B D E d M
Gọi giao điểm AC và d là M.
Xét tam giác AME và CME có:
^AME = ^CME = 90o
ME chung
AM = MC
\(\Rightarrow\Delta AME=\Delta CME\Rightarrow AE=CE\)
Hoàn toàn tương tự ta chứng minh được: \(\Delta\)AMD = \(\Delta\)CMD => AD = CD
Từ đây ta có: \(AE+EB=CE+EB>BC\left(\text{BĐT tam giác}\right)=CD+DB=AD+DB\)(đpcm)
Giải xong thầy chưa đọc hết bài nhưng nói quá dài dòng, không làm cách này! Nhưng theo mọi người thì cách em có đúng không? Có thể có cách nào ngắn gọn hơn không ạ?




Cách em làm đúng:)
Tuy nhiên nếu em học đường trung trực thì bài này có thể làm:
Ta có: A đối xứng với C qua đường thẳng d
=> d là đường trung trực của đoạn thẳng AC.
Do \(D\in d\Rightarrow DA=DC\)
Do \(E\in d\Rightarrow EA=EC\)
=> \(AD+DB=CD+BD=BC< BE+CE=BE+AE\)
=> Điều phải chứng minh.
Ngắn hơn đúng không :)
Nguyễn Linh Chi à đúng rồi! THầy em bảo dùng t/c đối xứng để làm:))