Cho hình chữ nhật ABCD tâm O. Gọi M,N lần lượt là trung điểm của OA và CD. Biết vecto MN= a.vecto AB+b.vecto AD. Tính a+b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\dfrac{3}{4}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{AB}=\dfrac{3}{4}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)-\dfrac{1}{2}\overrightarrow{AB}\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}\)
\(\Rightarrow a+b=\dfrac{1}{2}+\dfrac{3}{4}=...\)

Đáp án D
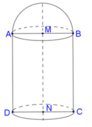
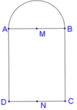
Khi quay mô hình đã cho quanh trục MN ta được một khối tròn xoay gồm:
- hình trụ có chiều cao là AD, đáy là hình tròn , có thể tích V 1 ;
- nửa hình cầu tâm M bán kính MA, có thể tích V 2
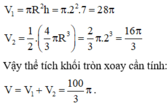

Đáp án C
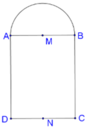
Khi quay mô hình đã cho quanh trục MN ta được một khối tròn xoay gồm:
- hình trụ có chiều cao là AD, đáy là hình tròn (M,MA), có thể tích V 1 ;
- nửa hình cầu tâm M bán kính MA, có thể tích V 2 .
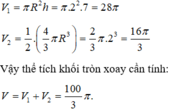
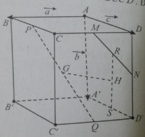
\(MC=\frac{3}{4}AC\Rightarrow\)\(\overrightarrow{MC}=\frac{3}{4}\overrightarrow{AC}\)
\(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AB}+\overrightarrow{AD}\) \(\Rightarrow\overrightarrow{MC}=\frac{3}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AD}\)
\(\overrightarrow{CN}=\frac{1}{2}\overrightarrow{CD}=-\frac{1}{2}\overrightarrow{AB}\)
\(\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\frac{3}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}=\frac{1}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AD}\)
\(\Rightarrow a+b=1\)