Cho tam giác ABC lấy M là trung điểm của BC . Lấy điểm I là trung điểm của AM. Kéo dài cắt AB ở D kẻ ME//CD. Chứng minh AD=DE=EB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

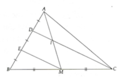
a) Xét ΔBCD có
M là trung điểm của BC
E là trung điểm của BD
Do đó: ME là đường trung bình của ΔBCD(Định nghĩa đường trung bình của tam giác)
Suy ra: ME//CD và \(ME=\dfrac{CD}{2}\)(Định lí 2 về đường trung bình của tam giác)
b) Xét ΔAEM có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM(Định lí 1 về đường trung bình của tam giác)
c) Xét ΔAEM có
D là trung điểm của AE
I là trung điểm của AM
Do đó: DI là đường trung bình của ΔAEM
Suy ra: DI//EM và \(DI=\dfrac{EM}{2}\)(Định lí 2 về đường trung bình của tam giác)
Ta có: \(DI=\dfrac{EM}{2}\)(cmt)
nên \(EM=2\cdot DI\)
\(\Leftrightarrow\dfrac{DC}{2}=2\cdot DI\)
\(\Leftrightarrow DC=4\cdot DI\)
\(\Leftrightarrow DC-DI=4DI-DI\)
\(\Leftrightarrow CI=3DI\)

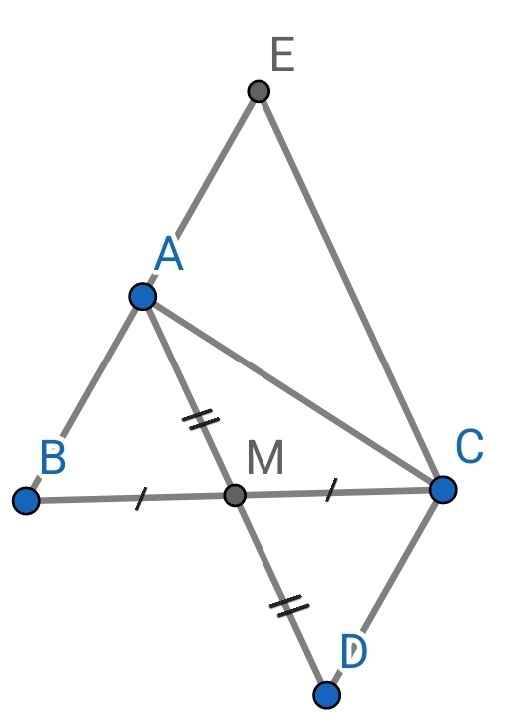 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Do M là trung điểm của AD (gt)
⇒ AM = MD
Xét ∆ABM và ∆DCM có:
AM = MD (cmt)
∠AMB = ∠CMD (đối đỉnh)
BM = MC (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
b) Do ∆ABM = ∆DCM (cmt)
⇒ ∠ABM = ∠CDM (hai góc tương ứng)
Mà ∠ABM và ∠CDM là hai góc so le trong
⇒ AB // CD
c) Do AB // CD (cmt)
⇒ ∠CAE = ∠ACD (so le trong)
∠ACE = ∠CAD (so le trong)
Xét ∆ACE và ∆CAD có:
∠ACE = ∠CAD (cmt)
AC là cạnh chung
∠CAE = ∠ACD (cmt)
⇒ ∆ACE = ∆CAD (g-c-g)
⇒ AE = CD (hai cạnh tương ứng)
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Mà AE = CD (cmt)
⇒ AB = AE
Vậy A là trung điểm của BE

a: Xét tứ giác ABCM có
E là trung điểm của đường chéo AC
E là trung điểm của đường chéo BM
Do đó: ABCM là hình bình hành
Suy ra: BC=AM

a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.
b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)
Tương tự, ta được: EM = (1/2)DC (2)
Từ (1) và (2) Þ DC = 4DI

a: Xét tứ giác ABCM có
E là trung điểm của đường chéo AC
E là trung điểm của đường chéo BM
Do đó: ABCM là hình bình hành
Suy ra: BC=AM

Xét ΔBDC có
M là trung điểm của BC
E là trung điểm của DB
Do đó: ME là đường trung bình của ΔBDC
Suy ra: ME//DC
Xét ΔAME có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM
hay AI=IM

Xét ΔBDC có
M là trung điểm của BC
E là trung điểm của BD
Do đó: ME là đường trung bình của ΔBDC
Suy ra: ME//DK
Xét ΔAEM có
D là trung điểm của AE
DK//EM
Do đó: K là trung điểm của AM
hay KA=KM