Cho hàm số \(y=x^4-2m^2x^2+2m^2-m\)(với m là tham số)
Xác định m để đồ thị hàm số đã cho có ba điểm cực trị là ba đỉnh của một tam giác có chu vi bằng \(2\left(1+\sqrt{2}\:\right)\)
.............................................................................
Cách của em như sau ạ, mong chị và mọi người hướng dẫn em với:
\(y=x^4-2m^2x^2+2m^2-m\)
\(y'=4x^3-4m^2x\)
\(y'=0\)\(\Leftrightarrow4x\left(x^2-m^2\right)=0\) \(\left(1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-m^2=0\left(2\right)\end{matrix}\right.\)
Đồ thị hàm số có 3 điểm cực trị khi và chỉ khi phương trình (1) có 3 nghiệm phân biệt
\(\Leftrightarrow\) phương trình (2) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow m>0\)
Với mọi \(m>0\) ta được \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-m^2=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=m\\x=-m\end{matrix}\right.\)
Gọi \(A\left(0;2m^2-m\right)\), \(B\left(m;-m^4+2m^2-m\right)\), \(C\left(-m;-m^4+2m^2-m\right)\)
Ta có: B và C đối xứng nhau qua Oy và A thuộc Oy
\(\Rightarrow AB=AC=\sqrt{m^2+m^8}\), \(BC=\sqrt{4m^2}\)
Chu vi tam giác ABC là bằng \(2\left(1+\sqrt{2}\: \right)\)khi và chỉ khi
\(AB+AC+BC=\)\(2\left(1+\sqrt{2}\: \right)\)
\(\Leftrightarrow\)\(2\sqrt{m^2+m^8}\)\(+\sqrt{4m^2}=\)\(2\left(1+\sqrt{2}\: \right)\)
............................................................
Đến đây làm sao tiếp nữa ạ

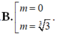



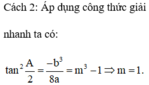
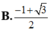
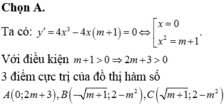


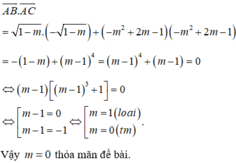
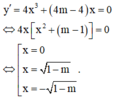
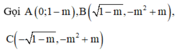
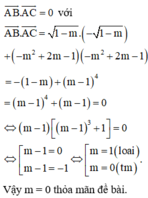
Nguyễn An: xin lỗi em chị trả lời hơi muộn.
Hướng đi của em hoàn toàn ổn và tự nhiên rồi, nhưng có 1 vài cái lưu ý là:
1. Điều kiện để PT(2) có 2 nghiệm pb là $m^2>0\Leftrightarrow m\neq 0$ chứ không phải $m>0$
2.
Đến đoạn $2\sqrt{m^2+m^8}+\sqrt{4m^2}=2(1+\sqrt{2})$
$\Leftrightarrow \sqrt{m^2+m^8}+|m|=1+\sqrt{2}$
$\Leftrightarrow \sqrt{t^2+t^8}-\sqrt{2}+t-1=0$ (đặt $|m|=t\geq 0$)
$\Leftrightarrow \frac{t^2+t^8-2}{\sqrt{t^2+t^8}+\sqrt{2}}+(t-1)=0$
$\Leftrightarrow (t-1)\left(\frac{t+1+t^7+t^6+...+1}{\sqrt{t^2+t^8}+\sqrt{2}}+1\right)=0$
Dễ thấy biểu thức trong ngoặc lớn luôn lớn hơn 0 với mọi $t\geq 0$
Do đó $t-1=0\Leftrightarrow |m|=t=1\Rightarrow m=\pm 1$ (thỏa mãn)
Thông thường những pt của mấy bài toán dạng này kiểu gì cũng ra nghiệm đẹp, nên dù thấy số ban đầu hơi xấu cũng đừng nản chí :v
@Akai Haruma chị ơi giúp em với