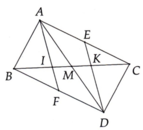
Cho tam giác ABC, E là trung điểm của AB, F thuộc AC: AF=2FC. Gọi M là trung điểm của BC và I là điểm thỏa mãn 4EI=3FI. Chứng minh A,M,I thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 10 2020
\(\overrightarrow{AF}=2\overrightarrow{FC}\Rightarrow\overrightarrow{AF}=\frac{2}{3}\overrightarrow{AC}\)
\(\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}\)
\(\overrightarrow{EI}=\frac{3}{4}\overrightarrow{IF}=\frac{3}{4}\left(\overrightarrow{IE}+\overrightarrow{EF}\right)\Rightarrow\overrightarrow{EI}=\frac{3}{7}\overrightarrow{EF}\)
\(\overrightarrow{AI}=\overrightarrow{AE}+\overrightarrow{EI}=\overrightarrow{AE}+\frac{3}{7}\overrightarrow{EF}=\overrightarrow{AE}+\frac{3}{7}\left(\overrightarrow{EA}+\overrightarrow{AF}\right)=\frac{4}{7}\overrightarrow{AE}+\frac{3}{7}\overrightarrow{EF}\)
\(\overrightarrow{AI}=\frac{4}{7}.\frac{1}{2}\overrightarrow{AB}+\frac{3}{7}.\frac{2}{3}\overrightarrow{AC}=\frac{2}{7}\overrightarrow{AB}+\frac{2}{7}\overrightarrow{AC}=\frac{4}{7}\left(\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}\right)=\frac{4}{7}\overrightarrow{AM}\)
\(\Rightarrow A;M;I\) thẳng hàng
6 tháng 12 2016
Giải
a) vì m la trung diểm của BC => BM=MC
Xét tam giac BAM va tam giac MAC có:
AB=AC(dề bài cho)
BM=MC(Chung minh tren)
AM la cạnh chung(de bai cho)
=>Tam giác BAM=tam giac MAC(c.c.c)
b)từ trên
=>góc BAM=góc MAC(hai goc tuong ung)
Tia AM nam giua goc BAC (1)
goc BAM=goc MAC(2)
từ (1) va (2)
=>AM la tia phan giac cua goc BAC
c)Còn nữa ......-->
21 tháng 2 2020
Bài làm
a) Xét tam giác AMN có:
AM = AN
=> Tam giác AMN cân tại A.
b) Xét tam giác ABC cân tại A có:
\(\widehat{B}=\frac{180^0-\widehat{A}}{2}\) (1)
Xét tam giác AMN cân tại A có:
\(\widehat{M}=\frac{180^0-\widehat{A}}{2}\) (2)
Từ (1) và (2) => \(\widehat{B}=\widehat{M}\)
Mà hai góc này ở vị trí đồng vị.
=> MN // BC
c) Xét tam giác ABN và tam giác ACM có:
AN = AM ( gt )
\(\widehat{A}\) chung
AB = AC ( Vì tam giác ABC cân )
=> Tam giác ABN = tam giác ACM ( c.g.c )
=> \(\widehat{ABN}=\widehat{ACM}\)( hai cạnh tương ứng )
Ta có: \(\widehat{ABN}+\widehat{MBC}=\widehat{ABC}\)
\(\widehat{ACM}+\widehat{MCB}=\widehat{ACB}\)
Mà \(\widehat{ABN}=\widehat{ACM}\)( cmt )
\(\widehat{ABC}=\widehat{ACB}\)( hai góc kề đáy của tam giác cân )
=> \(\widehat{IBC}=\widehat{ICB}\)
=> Tam giác BIC cân tại I
Vì MN // BC
=> \(\widehat{MNI}=\widehat{IBC}\)( so le trong )
\(\widehat{NMI}=\widehat{ICB}\)( so le trong )
Và \(\widehat{IBC}=\widehat{ICB}\)( cmt )
=> \(\widehat{MNI}=\widehat{NMI}\)
=> Tam giác MIN cân tại I
d) Xét tam giác cân AMN có:
E là trung điểm của MN
=> AE là trung tuyến
=> AE là đường trung trực.
=> \(\widehat{AEN}=90^0\) (1)
Xét tam giác cân MNI có:
E là trung điểm MN
=> IE là đường trung tuyến
=> IE là trung trực.
=> \(\widehat{IEN}=90^0\) (2)
Cộng (1) và (2) ta được:\(\widehat{IEN}+\widehat{AEN}=90^0+90^0=180^0\) => A,E,I thẳng hàng. (3)
Xét tam giác cân BIC có:
F là trung điểm BC
=> IF là trung tuyến
=> IF là trung trực.
=> \(\widehat{IFC}=90^0\)
Và MN // BC
Mà \(\widehat{IFC}=90^0\)
=> \(\widehat{IEN}=90^0\)
=> E,I,F thẳng hàng. (4)
Từ (3) và (4) => A,E,I,F thẳng hàng. ( đpcm )
# Học tốt #
6 tháng 11 2021
a, Vì E,F là trung điểm AC,BC nên EF là đtb tg ABC
Do đó EF//AB hay EF//AD và \(EF=\dfrac{1}{2}AB=AD\)(D là trung điểm AB)
Do đó AEFD là hbh
Vì AF là trung tuyến tam giác ABC cân tại A nên AF cũng là đường cao
Do đó AF⊥BC(1)
Lại có D,E là trung đỉm AB,AC nên DE là đtb tg ABC
Do đó DE//BC(2)
(1)(2) ta được DE⊥AF
Vậy AEFD là hthoi
b, Vì AEFD là hthoi mà I là trung điểm AF nên I là trung điểm DE
Vậy D,I,E thẳng hàng
16 tháng 12 2022
a: Xét ΔCAB có
M là trung điểm của CB
ME//BA
Do đó: E là trung điểm của AC
b: Xét tứ giác AFME có
AF//ME
AE//MF
Do đó: AFME là hình bình hành
=>AM cắt FE tại trung điểm của mỗi đường
=>E,O,F thẳng hàng
